Действительные числа

МАТЕМАТИЧЕСКИЙ АНАЛИЗ.

Оглавление.

1. Действительные числа.

2. Функция, понятие функции.

3. Предел числовой последовательности.

4. Предел функции.

5. Признаки существования пределов.

6. Бесконечно большие и бесконечно малые функции.

7. Замечательные пределы.

8. Непрерывные функции. Определение непрерывности.

9. Производная функции.

10. Основные правила дифференцирования.

11. Производные элементарных функций.

12. Геометрический смысл производной, уравнение касательной и нормали к кривой.

13. Дифференциал функции.

14. Применение дифференциального исчисления к исследованию функций. Локальный экстремум функции.

Простейшим множеством чисел является множество натуральных чисел 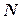- , которые вместе с отрицательными числами 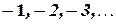и числом 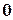образуют множество целых чисел .

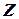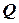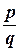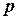Числа целые и дробные, как положительные, так и отрицательные составляют множество рациональных чисел. Каждое рациональное число может быть представлено в виде дроби , где и 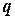- целые числа. Рациональные числа представляются в виде конечных и бесконечных периодических дробей. Все остальные числа называются иррациональными и представляются в виде бесконечных, непериодических дробей.

Свойства действительных чисел.

1. Между двумя действительными числами всегда находится рациональное и иррациональное.

2. Любое иррациональное число можно с любой степенью точности заменить рациональным.

Совокупность всех рациональных и иррациональных чисел образует множество действительных (вещественных) чисел.

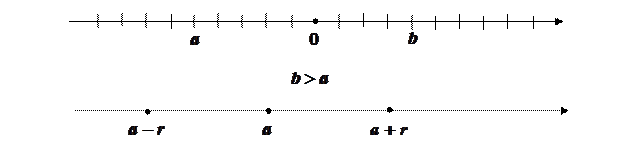
Числовая ось - это бесконечная прямая, на которой выбраны:

1). Некоторая точка 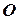, называемая началом отсчета.

2). Положительное направление, которое обозначается стрелкой.

3). Масштаб.

Действительные числа изображаются точками на числовой оси, и каждой точке числовой оси соответствует число.

Множество чисел, удовлетворяющих условию , называется интервалом и обозначается 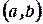или .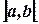

Множество чисел, удовлетворяющих условию 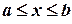, называется отрезком и обозначается .

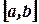Окрестностью точки на числовой оси называется интервал с центром в этой точке, 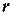- радиус интервала.

Дата добавления: 2014-10-15