Векторное произведение векторов. Векторное и смешанное произведение векторов

Векторное и смешанное произведение векторов

Тройка некомпланарных векторов, взятых в данном порядке, называется правой (левой), если кратчайший поворот от первого вектора ко второму из конца третьего виден против (по ходу) часовой стрелки.

Векторным произведением двух неколлинеарных векторов 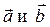, взятых в данном порядке, называют вектор 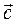, удовлетворяющий условиям:

1.

2.

3. 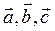- правая тройка векторов.

Запись: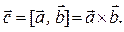

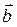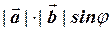Геометрический смысл векторного произведения: площадь параллелограмма, построенного на векторах и , численно равна длине вектора [], т.е. S_ð = | [ ] | = (19)

Свойства векторного произведения:

1⁰.

2⁰.

3⁰.

4⁰. .

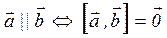Пример 1.12. Даны два вектора и , для которых . Найти: а), б).

Решение: а) (19) .

б) Воспользуемся свойствами векторного произведения:

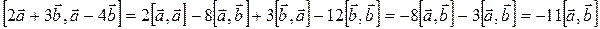
Следовательно: .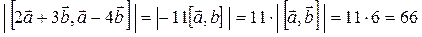

Ответ: а) 6; б) 66.

Векторное произведение в координатах: Пусть в ортонормированном базисе пространства 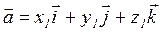, , 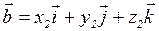тогда (20)

Здесь число 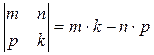- определитель второго порядка.

Приложения векторного произведения (вычисление площадей): Пусть Δ АВС задан в ПДСК О xyz координатами своих вершин:

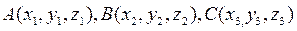. Тогда

(21)

Если z ₁= z ₂= z ₃=0, т.е. DАВСÎО xy, то

(21¢)

Пример 1.13. Найти координаты вектора если =(-3; 1; 2), =(-1; -2; 4).

Решение: Найдем координаты векторов:

,

.

Воспользуемся координатной формой векторного произведения:

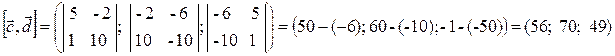
Ответ: (56; 70; 49).

Пример 1.14. Найти площадь треугольника с вершинами в точках

А(1; 2; 0), В(3; 0; -3), С(5; 2; 6).

Решение: Рассмотрим векторы и , совпадающие со сторонами треугольника: .

Используем геометрический смысл векторного произведения: .

Вычислим векторное произведение:

.

Найдем длину полученного вектора:

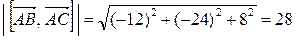Þ .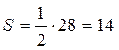

Ответ: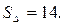

Дата добавления: 2014-10-22