Математическая модель задачи

Пример 1

Задача о назначениях.

В основе решения задачи о назначениях лежит венгерский алгоритм – алгоритм оптимизации, решающий задачу о назначениях за полиномиальное время. Он был разработан и опубликован Харолдом Куном в 1955 году.

Рассмотрим математическую модель и пример решения задачи.

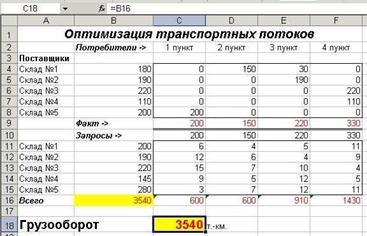
Рисунок 2.21 – Решенная транспортная задача

В конкурсе на занятие пяти вакансий (V1, V2, V3, V4, V5) участвуют семь претендентов (P1, P2, P3, P4, P5, P6, P7). Результаты тестирования каждого претендента, на соответствующие вакансии, даны в виде матрицы – С (тестирование производилось по десятибалльной системе).

Определить, какого претендента и на какую вакансию следует принять, причем так, чтобы сумма баллов всех претендентов оказалась максимальной.

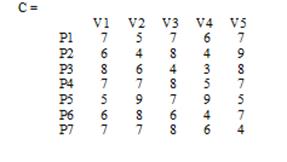
Рисунок 2.22 – Результаты тестирования претендентов

1) Переменные задачи.

Введем переменные x_ij принимающие два значения:

x_ij = 0, если i -й претендент (P_i) не принимается на j -ю вакансию (V_j).

x_ij = 1, если i -й претендент (P_i) принимается на вакансию (V_j).

i = 1,2,...7; j = 1,2,...5.

2) Ограничения на переменные задачи.

Очевидно, что все переменные задачи неотрицательные и целые числа: x_ij 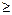0 и x_ij – целые.

Кроме того, так как каждый претендент может занять только одну вакансию и все вакансии должны быть заняты, должны удовлетворяться следующие ограничения:

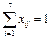, j = 1,2,...7,

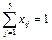, i = 1,2,...5,

Другими словами в матрице (x_ij) суммы элементов по каждой строке и суммы элементов по каждому столбцу должны быть равны единицам. Это условие означает, что выбор претендентов должен быть таким, чтобы в матрице (x_ij), представляющей решение задачи, было бы по одной единице в каждой строке и по одной единице в каждом столбце, остальные элементы матрицы должны равняться нулю.

3) Целевая функция в задаче о назначениях.

Необходимо выбрать претендентов так, чтобы суммарное число очков, набранное ими было бы максимальным. Суммарное число набранных очков вычисляется по формуле:

;

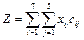Z = c₁₁x₁₁ + c₁₂x₁₂ +...+ c₇₅x₇₅ = 7 x₁₁ + 5 x₁₂ +... + 4 x₇₅;

Окончательная математическая модель задачи записывается так:

найти max ;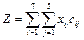

при ограничениях:

x_ij 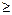0 и x_ij – целые числа, i = 1,2,...7; j = 1,2,...5;

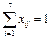, j = 1,2,...7;

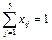, i = 1,2,...5.

Таким образом, задача о назначениях есть частный случай транспортной задачи.

Дата добавления: 2014-10-22