Решение задачи о назначениях при помощипреобразования матрицы (С)

Рассмотрим решение задачи о назначениях, в которой нужно найти min функции Z. Предварительно задачу о назначениях нужно сбалансировать. В рассматриваемом примере эта процедура выполняется добавлением двух столбцов (две фиктивные вакансии) с нулевыми результатами тестирования:

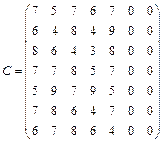
Задача нахождения минимального значения функции Z эквивалентна задаче нахождения минимума для функции 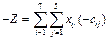, матрица (– С) имеет вид:

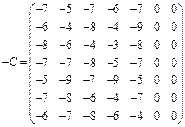
Нетрудно показать, что при вычитании из всех элементов столбца или строки матрицы (С) одного и того же числа, решения x_ij при которых функция 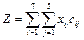имеет минимум не меняется. Поэтому матрицу (С) преобразуем по следующему правилу. В каждой строке (С) и в каждом столбце образуют нули, вычитая минимальные элементы из соответствующих строк или столбцов. Если среди нулевых элементов матрицы (С) можно получить допустимое решение задачи, то оно является оптимальным. Напомним, что допустимым решением является такой выбор из нулей, при котором выбирается по одному нулю в каждой строке и по одному нулю в каждом столбце.

В рассматриваемом примере в каждой строке матрицы (С) нули есть (они появились в результате добавления фиктивных вакансий). Чтобы образовать нули в первых пяти столбцах матрицы (– С), определяем минимальные элементы в этих столбцах: -8, -9, -8, -9, -9 и вычитаем эти элементы из соответствующих столбцов матрицы. В результате получим следующую матрицу (рис. 2.23):

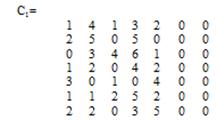
Рисунок 2.23 – Матрица результатов

Так как из нулевых элементов нельзя получить допустимое решение (в первой и шестой строках, а также в четвертой и седьмой строках нули стоят на одном и том же месте), то алгоритм продолжается следующим образом:

a) минимальным количеством горизонтальных и вертикальных прямых вычеркиваем все нули.

b) среди не вычеркнутых элементов находим минимальный элемент;

c) вычитаем минимальный элемент из всех вычеркнутых элементов;

d) к элементам, стоящим на пересечении вертикальных и горизонтальных прямых, прибавляем минимальный элемент.

Среди множества получаемых нулевых элементов определяем допустимое решение. Если допустимое решение найти нельзя, повторяем шаги a, b, c, d снова.

Процедура вычеркивания элементов и ее результат показаны на рис. 2.24. Минимальный среди не вычеркнутых элементов равен единице.

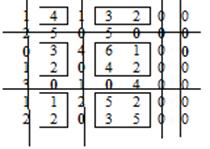
Рисунок 2.24 – Процедура вычеркивания элементов

На рис. 2.25 показан результат после вычитания единицы из не вычеркнутых элементов и прибавления единицы к элементам, стоящим на пересечении прямых. Допустимое решение соответствует отмеченным элементам.

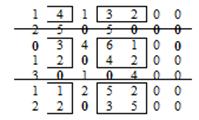
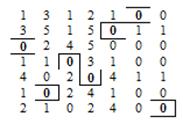
Рисунок 2.25 – Допустимое решение

Перенеся полученное решение на исходную матрицу (С) (рис. 2.26):

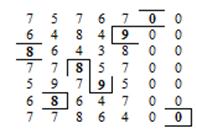
Рисунок 2.26 – Оптимальное решение

Получим, что претенденты Р 1 и Р 7попадают на фиктивные вакансии и не принимаются на работу. Р 2 принимается на пятую вакансию, Р 3 – на первую, Р 4 – на третью, Р 5 – на четвертую, Р 6 – на вторую. Сумма баллов, полученная при данном решении равна: 9 + 8 + 8 + 9 + 8 = 42.

Дата добавления: 2014-10-22