Пример 2. Определить оптимальное соотношение между вариантами технологического процесса и конструктивного выполнения изделия

Определить оптимальное соотношение между вариантами технологического процесса и конструктивного выполнения изделия.

Существует четыре варианта конструктивного выполнения изделия и четыре варианты технологического процесса его изготовления, любой из которых оценивается по 5 критериям. Любой из критериев имеет по три оценки в своей шкале.

В результате расчетов и экспертных оценок полученные многочисленные значения оценок вариантов конструктивного выполнения изделия по показателям назначения и оценок вариантов технологического процесса его изготовление по показателям технологичности.

Многочисленные значения оценок для конструктивного варианта изделия Qі приведены в табл. 2.5. Для технологического процесса С_і – в табл. 2.6.

Таблица 2.5 – Многочисленные значения оценок для конструктивного варианта изделия

	К 1	К 2	К 3	К 4	К 5
Q 1
Q 2
Q 3
Q 4

Таблица 2.6 – Многочисленные значения оценок для технологического процесса изготовления изделия

	К 1	К 2	К 3	К 4	К 5
С 1
С 2
С 3
С 4

Решаем задачу, используя методику решения многокритериальных задач о назначении.

Основой многокритериальных задачи о назначении является вектор соотношения:

,

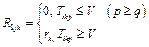где Т_і.kp – требования і -го элемента однго множества, которые выражены p -ю оценкой на шкале требований по k -тому критерию; V_i.kq – соотношение возможности j -го элемента другого множества, которое выражено q -ю оценкой по шкале возможностей того же k -го критерия; r_k – число оценок на шкале k -го критерия, на которой требования превышают возможности.

Свертка вектора соотношения:

0 – пары с полностью удовлетворяющими требованиями по всем критериям;

1 – неудовольствие одного из требований, причем степень неудовольствия равняется одной градации шкалы;

2 – неудовольствие одного из требований на две градации шкалы.

Строим матрицу векторов соотношения.

Таблица 2.7 – Матрица векторов соотношения

	C 1	C 2	C 3	C 4
Q 1
Q 2
Q 3
Q 4

Строим матрицу индексов соотношения.

Таблица 2.8 – Матрица индексов соотношения

	C 1	C 2	C 3	C 4
Q 1
Q 2
Q 3
Q 4

Определяем оптимальное соотношение критериев с помощью Венгерского метода.

В матрицы индексов соотношения определяем в каждой строчке минимальное значение и отнимаем его от других элементов строки.

Таблица 2.9 – Определение минимума по строкам

	C 1	C 2	C 3	C 4	Минимум по строкам
Q 1
Q 2
Q 3
Q 4

Таблица 2.10 – Матрица оптимального соотношения

	C 1	C 2	C 3	C 4
Q 1
Q 2
Q 3
Q 4

Оптимальным значением отвечают нулевые элементы, полученные в процессе преобразования матрицы индексов соотношения.

Оптимальными соотношениями конструктивного выполнения изделия и технологического процесса его изготовление есть: Q ₁ – C ₂, Q ₂ – C ₄, Q ₃ – C ₃, Q ₄ – C ₁.

Дата добавления: 2014-10-22