Вопрос 5.3. Системы линейных алгебраических уравнений

Коней примера.

Определение 5.2. Системой линейных алгебраических уравнений называется система вида

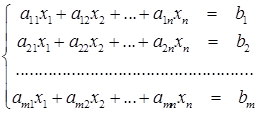
Числа 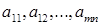называются коэффициентами системы уравнений. Числа 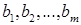называются правыми частями системы уравнения. Величины называются неизвестными, их число может не равняться числу уравнений.

Определение 5.3. Решением системы называются любые числа , которые при подстановке в систему уравнений обращают каждое уравнение в верное числовое равенство.

Определение 5.4. Матрицей коэффициентов системы линейных алгебраических уравнений называется матрица

Определение 5.5. Столбцом неизвестных и столбцом правых частей называются соответственно следующие матрицы

Используя матричное исчисление, систему линейных уравнений можно записать в виде одного матричного уравнения

.

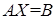Определение 5.6. Система линейных уравнений называется однородной, если все ее правые части равны нулю и неоднородной в противном случае.

Определение 5.7. Система линейных уравнений называется совместной, если она имеет хотя бы одно решение.

Определение 5.8. Система линейных уравнений называется несовместной, если она не имеет решений.

Определение 5.9. Совместная система линейных уравнений называется определенной, если она имеет ровно одно решение.

Определение 5.10. Совместная система линейных уравнений называется неопределенной, если она имеет несколько решений.

Дата добавления: 2014-10-22