Конец доказательства

Конец доказательства.

Теорема 7.2. При сложении векторов их координаты складываются, а при вычитании ‑ вычитаются. При умножении на число координаты вектора умножаются на это число.

Доказательство. Если вектора 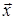и 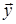разложены по базису, то

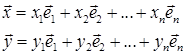
Складывая вектора 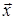и 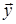, получим

Аналогично доказываются два последних утверждения.

Определение 7.10. Параллельные друг другу вектора называются коллинеарными.

Очевидно, что если вектора 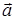и 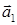коллинеарны, то . При этом 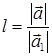, если вектора 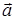и 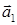одинаково направлены и 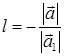в противном случае. Отсюда следует, что два коллинеарных вектора линейно зависимы, так как можно записать

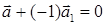
Справедливо обратное утверждение: два линейно зависимых вектора коллинеарны. Действительно, пусть

и, например, коэффициент 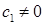, тогда

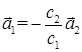
Из выше сказанного следует, что два неколлинеарных вектора линейно независимы.

Определение 7.11. Три вектора, параллельные одной и той же плоскости, называются компланарными.

Теорема 7.3. На плоскости любые два неколлинеарных вектора образуют базис.

Доказательство. Пусть даны два произвольных неколлинеарных вектора 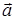и 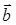, лежащие в одной плоскости. Покажем, что произвольный плоский вектор 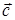можно разложить по этим векторам. Проведем через конец вектора 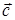две прямые, параллельные векторам 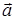и 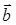. Тогда вектор 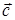есть сумма векторов 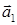и 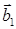(см. рис. 2).

Рис. 2. К доказательству теоремы 3.

Но вектора 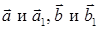коллинеарны, поэтому 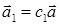и . Тогда 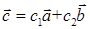. Кроме того, вектора 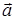и 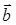как неколлинеарные линейно независимы. Таким образом, произвольный вектор 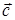разлагается по линейно независимым векторам 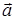и 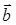. Следовательно, вектора 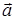и 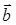образуют базис на плоскости.

Дата добавления: 2014-10-22