Вопрос 9.1. Векторное произведение

ВЕКТОРНАЯ АЛГЕБРА.

Конец примера.

Пример 8.2.

Конец примера.

Механический смысл скалярного произведения:

‑ работа силы по перемещению тела на вектор перемещения .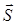

Определение 9.1. Три вектора образуют правую тройку векторов при условии, что вращение первого вектора ко второму на наименьший угол происходит против часовой стрелки, если смотреть из конца третьего (рис. 1 а)).

Рис. 1. a) Правая тройка.

б) Геометрический смысл векторного произведения.

Определение 9.2. Вектор является векторным произведением векторов , если

1) вектора образуют правую тройку,

2) вектор перпендикулярен векторам ,

3) длина вектор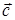а равна 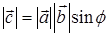, где f ‑ угол между векторами.

Векторное произведение обозначается так

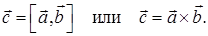
Геометрический смысл векторного произведения: длина векторного произведения равна площади параллелограмма, построенного на векторах или равна удвоенной площади треугольника, построенного на тех же векторах (см. рис. 1 b)). Механический смысл векторного произведения раскрывается формулой момента силы относительно начала координат

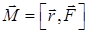
где

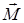‑ момент силы,

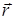‑ радиус-вектор,

‑ сила.

Свойства векторного произведения:

1) ,

2) ,

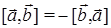3) 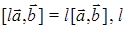‑ числовой множитель,

4) .

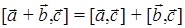Свойство 1) справедливо, поскольку угол между векторами равен 0. Свойство 2) есть следствие того, что при перестановке векторов нужно изменить направление вектора 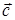на противоположное для того, что бы тройка векторов осталась правой. Свойство 3) так же легко обосновать (сделайте это сами!). Свойство 4) приводится без доказательства.

Пусть вектора разложены по базису

тогда

Так как перпендикулярные друг другу вектора единичной длины, то, пользуясь определением векторного произведения, легко получить, что (см. рис. 2)

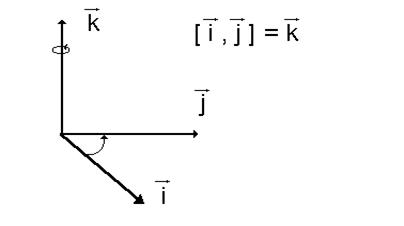
Рис. 2. Векторное произведение базисных векторов декартовой системы координат.

б

Отсюда получим

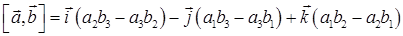
или

.

Эту формулу можно переписать в виде определителя

.

В заключение приведем формулу двойного векторного произведения:

.

Дата добавления: 2014-10-22