
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопрос 11.1. Прямая на плоскости
|
|
|
|
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.
Конец доказательства.
Конец доказательства.
Свойство 10.4. Циклическая перестановка векторов в смешанном произведении не меняет его величины.
Доказательство. Циклическая перестановка ‑ это перестановка, в которой первый объект становится третим, второй ‑ первым, третий вторым
1 2 3 Þ 2 3 1.
Циклическую перестановку можно представить как композицию двух перестановок соседних объектов:
1 2 3 Þ 2 1 3 Þ 2 3 1
Тогда знак смешанного произведения согласно свойству 10.3 будет меняться дважды, и в конечном итоге останется без изменения.
Пусть прямая L лежит в плоскости P. Выберем декартову систему координат на плоскости XY так, чтобы ось X совпадала бы с прямой L. Тогда уравнение прямой L будет иметь вид  . Найдем уравнение прямой L в произвольной декартовой системе координат на плоскости P. Рассмотрим вспомогательную лемму.
. Найдем уравнение прямой L в произвольной декартовой системе координат на плоскости P. Рассмотрим вспомогательную лемму.
Лемма 11.1. Пусть на плоскости P заданы две произвольные системы координат CS и 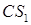 . Тогда координаты произвольной точки M плоскости P в системе координат CS и
. Тогда координаты произвольной точки M плоскости P в системе координат CS и 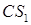 связаны соотношением
связаны соотношением
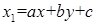 , (1)
, (1)
 . (2)
. (2)
 образуют базис соответственно для систем координат CS и
образуют базис соответственно для систем координат CS и 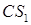 (см. рис. 1).
(см. рис. 1).
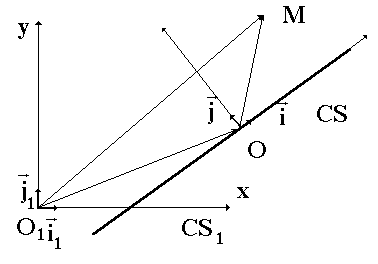
Рис. 1. К доказательству леммы 1.
Разложим вектора первого базиса по векторам второго базиса
 , (3)
, (3)
 . (4)
. (4)
Радиус-векторы точки M в системах координат CS и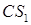 связаны равенством
связаны равенством
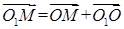 (5)
(5)
где O и  начала координат для CS и
начала координат для CS и 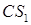 . Разложим радиус-векторы по базисным векторам
. Разложим радиус-векторы по базисным векторам
 , (6)
, (6)
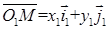 , (7)
, (7)
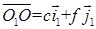 . (8)
. (8)
Тогда, подставляя формулы (6)-(8) в формулу (5), получим
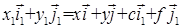 . (9)
. (9)
С помощью соотношений (3) и (4) преобразуем (9) в равенство

Перенесем все величины в правую часть равенства и сгруппируем слагаемые, тогда получим

Откуда получаем в силу линейной независимости векторов
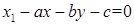 ,
,
 ,
,
что эквивалентно уравнениям (1) и (2).
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 371; Нарушение авторских прав?; Мы поможем в написании вашей работы!