Уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору

Конец доказательства.

Рассмотрим теперь различные типы уравнений прямой на плоскости.

1) Общее уравнение плоскости P.

Из вывода уравнения следует, что одновременно A, B и C не равны 0 (объясните почему).

Точка 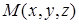принадлежит плоскости P только в том случае, когда ее координаты удовлетворяют уравнению плоскости. В зависимости от коэффициентов A, B, C и D плоскость P занимает то или иное положение:

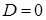‑ плоскость проходит через начало системы координат,

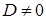‑ плоскость не проходит через начало системы координат,

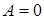‑ плоскость параллельна оси X,

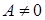‑ плоскость не параллельна оси X,

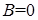‑ плоскость параллельна оси Y,

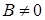‑ плоскость не параллельна оси Y,

‑ плоскость параллельна оси Z,

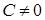‑ плоскость не параллельна оси Z.

Докажите эти утверждения самостоятельно.

(6)

Здесь 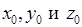‑ координаты точки M, лежащей на плоскости P, A, B и C ‑ координаты вектора, перпендикулярного плоскости P. Этот вектор называется нормальным к плоскости P (см. рис. 1).

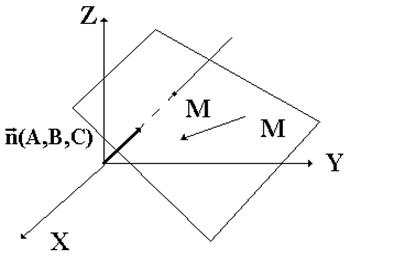
Рис. 1. К выводу общего уравнения плоскости.

Уравнение (6) легко выводится из уравнения (5). Действительно, пусть точка лежит на плоскости P. Тогда ее координаты удовлетворяют уравнению

. (7)

Вычитая из уравнения (5) уравнение (7) и группируя слагаемые, получим уравнение (6). Рассмотрим теперь два вектора с координатам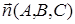и и соответственно. Из формулы (6) следует, что их скалярное произведение равно нулю. Следовательно, вектор 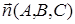перпендикулярен вектору . Начало и конец последнего вектора находятся соответственно в точках и 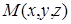, которые принадлежат плоскости P. Следовательно, вектор 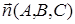перпендикулярен плоскости P.

Расстояние от точки до плоскости P, общее уравнение которой 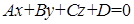, определяется по формуле

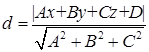(8)

Доказательство этой формулы полностью аналогично доказательству формулы расстояния между точкой и прямой (см. рис. 2).

Рис. 2. К выводу формулы расстояния между плоскостью и прямой.

Действительно, расстояние d между прямой и плоскостью равно

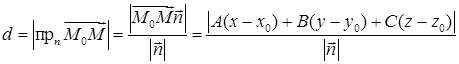
где ‑ точка лежащая на плоскости. Отсюда, как и в лекции № 11, получается выше приведенная формула. Две плоскости параллельны, если параллельны их нормальные вектора. Отсюда получаем условие параллельности двух плоскостей

(9)

где

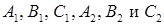‑ коэффициенты общих уравнений плоскостей 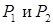. Две плоскости перпендикулярны, если перпендикулярны их нормальные вектора, отсюда получаем условие перпендикулярности двух плоскостей, если известны их общие уравнения

(10)

Угол f между двумя плоскостями равен углу между их нормальными векторами (см. рис. 3) и может, поэтому, быть вычислен по формуле

Рис. 3. Определение угла между плоскостями.

(11)

Дата добавления: 2014-10-22