Предел функции. Определение 16.15. Число A называется пределом функции в точке b, если для любой последовательности аргументов

Определение 16.15. Число A называется пределом функции 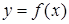в точке b, если для любой последовательности аргументов, сходящийся к точке b и неравных b

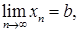
последовательность значений функции сходится к A

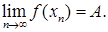
Это определение предела функции по Гейне (через предел последовательности). Можно дать другое определение предела функции по Коши.

Определение 16.16. Число A называется пределом функции 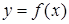в точке b, если для любого 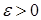существует 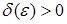такое, что для всех x, удовлетворяющих неравенству

,

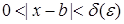выполняется неравенство

.

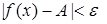Предел функции обозначается следующим образом

.

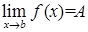Нетрудно доказать, что оба определения предела функции эквивалентны. Действительно, пусть существует предел функции по Коши, тогда, если последовательность аргументов сходится к любого 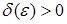существует число 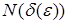такое, что для всех 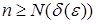выполняется неравенство

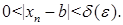
Тогда, в силу существования предела по Коши, справедливо неравенство

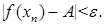
Аналогично доказывается обратное утверждение.

Используя определение предела функции по Гейне через предел последовательности, можно легко распространить определение предела на случай бесконечно удаленной точки или на случай бесконечно большого предельного значения функции, то есть определить следующие конструкции предельных переходов:

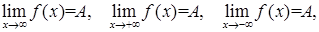
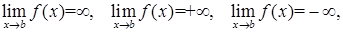
где b конечное число или бесконечность .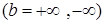

Можно построить определение таких предельных переходов по Коши и доказать их эквивалентность.

Из определения предела функции в конечной или бесконечной точке следует выполнение следующих свойств предела функций

1) 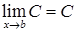, где ;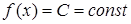

2)

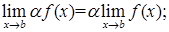
Если существуют пределы 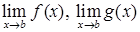, то

3)

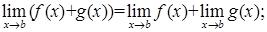
4)

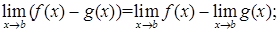
5)

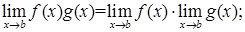
6) 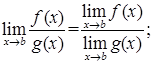где .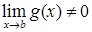

Дата добавления: 2014-10-22