Конец доказательства

Конец доказательства.

Доказательство.

Вопрос 10.2. Свойства смешанного произведения.

Конец доказательства.

Из теоремы 10.1 получаем условие компланарности трех векторов:

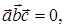
а так же условие принадлежности четырех точек пространства 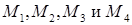одной плоскости

.

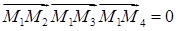Свойство 10.1. Смешанное произведение линейно по каждому множителю

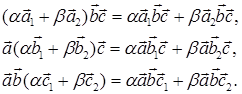
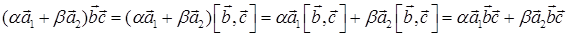
Аналогично доказываются две другие формулы.

Свойство 10.2. Смешанное произведение векторов равно определителю третьего порядка, составленного из декартовых координат этих векторов

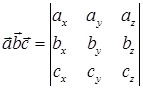, где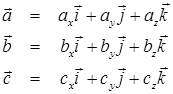

Доказательство. По определению смешанного произведения

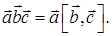
Так как

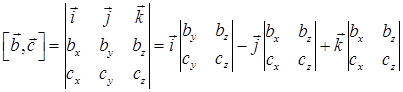
то, вычисляя скалярное произведение, получим

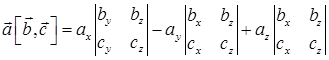
или

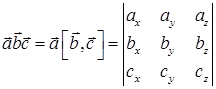
Свойство 10.3. Перестановка двух соседних множителей в смешанном произведении меняет его знак на противоположный.

Доказательство. Перестановка двух соседних множителей эквивалентна перестановке соседних строк определителя, составленного из координат векторов. Как известно, такая перестановка меняет знак определителя на противоположный, а, следовательно, и знак самого смешанного произведения.

Дата добавления: 2014-10-22