Нелинейность, заданная в угле

Критерий абсолютной устойчивости определяет условия абсолютной устойчивости.

Критерий абсолютной устойчивости Попова

Алгоритм решения

1) Строим графики АФХ линейной части и инверсной ЭКАЧХ.

2) Находим точки пересечения двух графиков.

3) Определяем частоту по АФХ линейной части, а амплитуду – по кривой .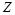

Если кривые пересекаются в нескольких точках, то возможно несколько автоколебательных режимов.

4) Определяем устойчивость предельных циклов.

Правило: предельный цикл в системе будет устойчивым, если изображающая точка при перемещении по кривой 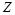в направлении возрастания амплитуды подходит к точке пересечения двух графиков изнутри характеристики .

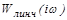Пример:

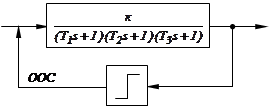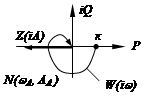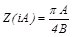
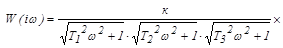
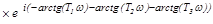
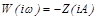
В данной системе возможны автоколебания с частотой 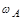и амплитудой 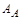и предельные циклы, им соответствующие, являющиеся устойчивыми.

у_н.э.

Нелинейность задается не конкретной статической характеристикой, а в более общем виде – в виде принадлежности к классу (речь идет о существенных нелинейностях).

a

b

х

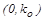Статическая характеристика нелинейности, заданная в угле , должна находиться между осью абсцисс и прямой 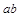с угловым коэффициентом 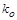. Заданная таким образом статическая характеристика неоднозначна относительно своего вида, но безынерционна и однозначна относительно входа нелинейного элемента.

Модифицированная АФХ – это АФХ линейной части системы, полученная из обычной АФХ путем умножения мнимой части на частоту.

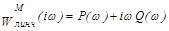
Статическую характеристику можно записать как условие принадлежности к классу в виде:

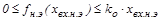
Рассмотрим систему в виде:

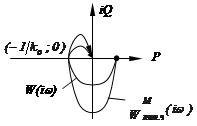Состояние равновесия системы с однозначной нелинейной характеристикой, заданной в угле 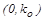, и устойчивой линейной частью будет устойчивым, если через точку 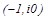можно провести хотя бы одну прямую, пересекающую вещественную полуось так, что годограф модифицированной АФХ целиком располагается справа от этой прямой. Такая прямая называется линией Попова.

Дата добавления: 2014-10-22