Метод гармонической линеаризации

Данный метод применяется для определения наличия автоколебаний и их параметров (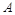и 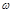). Исследование проводится для гармонически линеаризованной системы.

Суть гармонической линеаризации базируется на том, что все высокочастотные гармоники оказывают на САР малое влияние, т.е. объекты регулирования являются низкочастотными фильтрами, т.к. вид АЧХ реального объекта – это кривая, стремящаяся к нулю при .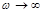

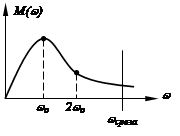Гипотеза фильтра выполняется, если:

Гармоническая линеаризация позволяет создать эквивалентную линейную модель, которая при обработке гармонического сигнала ведет себя, как исходная нелинейная система.

Моделью автоколебаний является режим нахождения на границе устойчивости эквивалентной системы.

Метод гармонической линеаризации применяется для линеаризации существенных нелинейностей и для случаев, когда неприменим метод Тейлора. На вход такой системы подаются синусоидальные колебания, тогда на выходе получаем периодическую функцию, которую можно разложить в ряд Фурье.

;

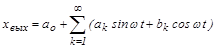
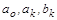– коэффициенты разложения в ряд Фурье.

По линейности системы 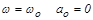, где – основная частота.

Если на вход линейной системы, для которой выполняется гипотеза фильтра, подать синусоидальный сигнал, то она воспримет только гармонику с частотой :

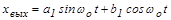
В нелинейной системе выделяют линейную часть и нелинейный элемент.

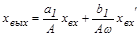
Применим преобразование Лапласа к левой и правой частям:

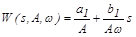– эквивалентная передаточная функция.

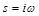
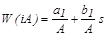– эквивалентная комплексная АЧХ (ЭКАЧХ).

Для частных случаев нелинейных элементов известны ЭКАЧХ. Например:

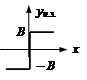– для элемента идеальное реле:

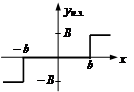– для трехпозиционного реле:

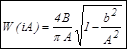
В расчетах используется понятие инверсной ЭКАЧХ, т.е.: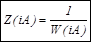

Дата добавления: 2014-10-22