Решение. Здесь выполняются следующие операции:

Решение

Здесь выполняются следующие операции:

1) находится величина, обратная x: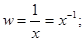

2) от w берется косинус: ;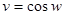

3) от v берется логарифм: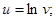

4) u возводится в степень с показателем : .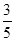

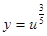Последняя операция здесь - возведение в степень .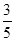

Пример 4. Записать зависимость y от x в виде цепочки основных элементарных функций, если: .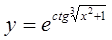

Здесь выполняются следующие операции:

1) возведение x в квадрат и сложение результата с единицей: ;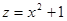

2) извлечение корня: ;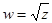

3) взятие котангенса: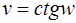

4) возведение в куб: ;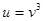

5) взятие показательной функции: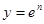

Итак: ; ; ; ; .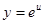

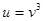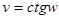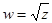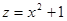Последняя операция - взятие показательной функции.

При дифференцировании сложной функции нужно выделить последнюю операцию в ее аналитическом выражении, и объект этой операции (т.е. величину, над которой операция производится) обозначить буквой, например, «u». Это «u» будет играть роль промежуточной переменной, Затем следует применить правило (2). Потом снова выделить последнюю операцию уже в промежуточной функции и опять применить формулу (2) и т.д.

Пример 5. Найти производную функции .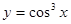

Дата добавления: 2014-10-22