
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнение колебаний струны
|
|
|
|
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
Определить тип уравнения и привести к каноническому виду
1. 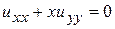 . 2.
. 2. 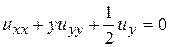 . 3.
. 3. 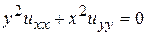 .
.
4. 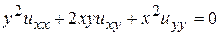 . 5.
. 5.  .
.
6.  .
.
7. 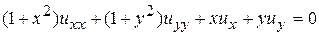 .
.
Рассмотрим струну, под которой понимается тонкая нить, не сопротивляющаяся изгибу, длиной l. Пусть эта струна в плоскости (x,u) совершает малые поперечные колебания около своего положения равновесия, совпадающего с осью Ох, то есть все точки струны движутся перпендикулярно оси Ох. Обозначим через u(x,t) отклонение от положения равновесия точки струны с абсциссой х в момент времени t. Так как струна не сопротивляется изгибу, то ее натяжение 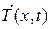 в точке х в момент времени t направлено по касательной к струне в точке х. Любой участок струны (а,b) после отклонения от положения равновесия в предположении о пренебрежении величинами высшего порядка малости по сравнению с
в точке х в момент времени t направлено по касательной к струне в точке х. Любой участок струны (а,b) после отклонения от положения равновесия в предположении о пренебрежении величинами высшего порядка малости по сравнению с 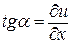 , не изменит своей длины
, не изменит своей длины
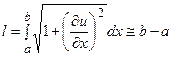 (16)
(16)
и, следовательно, величина натяжения 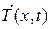 будет постоянной Т 0, не зависящей от х и t, так как закон Гука гласит: изменение натяжения пропорционально изменению длины выделенного участка.
будет постоянной Т 0, не зависящей от х и t, так как закон Гука гласит: изменение натяжения пропорционально изменению длины выделенного участка.
Составим уравнение движения струны. На элемент струны (х, 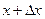 ) действуют силы натяжения
) действуют силы натяжения  и внешняя сила
и внешняя сила 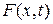 , действующая на струну в точке х в момент времени t и направленная перпендикулярно оси Ох.
, действующая на струну в точке х в момент времени t и направленная перпендикулярно оси Ох.
Сумма сил, действующих на струну, согласно закону Ньютона должна быть равна произведению массы элемента струны на его ускорение
 , (17)
, (17)
где 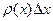 - масса элемента струны (х,
- масса элемента струны (х, 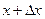 );
);
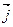 - единичный вектор, направленный вдоль оси u.
- единичный вектор, направленный вдоль оси u.
Проектируя векторное равенство (17) на ось u, получим
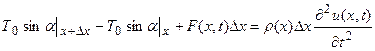 , (18)
, (18)
но в рамках приближения
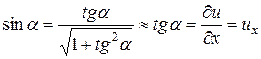 ,
,
поэтому выражение (18) принимает вид

и при  , получим
, получим
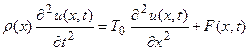 . (19)
. (19)
Это и есть уравнение малых поперечных колебаний струны. Если F(x,t)¹ 0, то колебания струны будут вынужденными, а если F(x,t)= 0, то колебания струны будут свободными.
Если 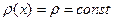 , то уравнение (19) принимает вид
, то уравнение (19) принимает вид
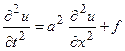 , (20)
, (20)
где 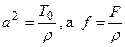 .
.
Уравнение (20) называется одномерным волновым уравнением. Для волнового уравнения может быть поставлена задача Коши, и в этом случае необходимо найти функцию u(x,t), удовлетворяющую начальным условиям
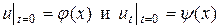
где 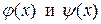 - заданные функции.
- заданные функции.
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 915; Нарушение авторских прав?; Мы поможем в написании вашей работы!