Решение краевых задач методом Фурье

Рассмотрим задачу отыскания нестационарного температурного поля u (x,t) в плоском слое конечной толщины l, имеющим в начальный момент времени температуру , если на поверхностях x=0 и l=0 этого слоя происходит теплообмен с окружающей средой, имеющей нулевую температуру. Требуется найти решение однородного линейного параболического уравнения

, (84)

удовлетворяющее при t =0 начальному условию

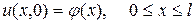, (85)

и однородным граничным условиям третьего рода

(86)

Нетривиальные решения уравнения (84), удовлетворяющие граничным условиям (86), будем искать в виде

. (87)

Подставив эту форму решения в уравнение (84) и разделив переменные, получим

.

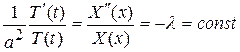Поэтому функции T (t) и X (x) можно найти как решения обыкновенных однородных дифференциальных уравнений вида

; (88)

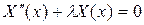. (89)

Рассмотрим уравнение (89) с граничными условиями вида

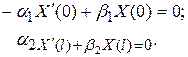(90)

Задача (89)-(90) является задачей Штурма-Лиувилля. Для того, чтобы найти собственные значения, необходимо найти нетривиальные решения уравнения (89). Поскольку корни характеристического уравнения, соответствующего уравнению (89) исключительно мнимые 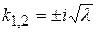, то общее решение уравнения (89) имеет вид

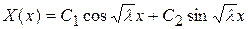. (91)

Вычислим производную от (91) и, удовлетворив краевым условиям (90), получим

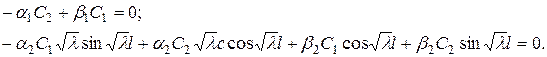Из первого равенства выразим С ₁ и подставим во второе уравнение

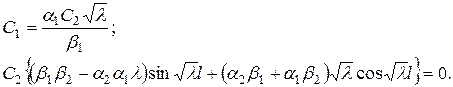
Из второго уравнения системы следует, что, если С ₂ =0, то и С ₁ тоже будет равна нулю. Следовательно, X (x) ≡ 0., поэтому нетривиальные решения уравнения (89) будут при условии, что

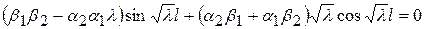. (92)

Таким образом, задача Штурма-Лиувилля (89), (90) имеет нетривиальные решения только при определенных, собственных значениях

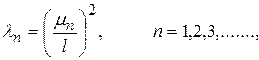(93)

которые можно выразить через неотрицательные корни 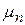, полученного из условия (92), трансцендентного уравнения вида

.

Соответствующие собственным значениям 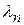собственные функции X_n (x) имеют вид

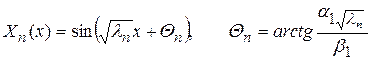. (94)

Квадраты норм этих функций определяются выражением

.

При 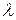=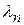уравнение (88) принимает вид

.

Общее решение этого однородного линейного уравнения имеет вид

. (95)

Таким образом, подставляя (94) и (95) в (87) получим частные решения уравнения (84), удовлетворяющие краевым условиям (86):

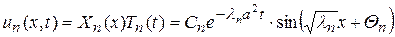. (96)

На основании принципа суперпозиции частных решений следует, что общее решение уравнения (84) может быть представлено в области в виде ряда

. (97)

Рассмотрим частные случаи задачи (84)-(86).

1. При значении параметров краевые условия принимают вид

(98)

и краевая задача (84),(85), (98) описывает процесс остывания плоского слоя конечной толщины l (или стержня конечной длины l с идеально теплоизолированной боковой поверхностью), с температурным профилем 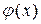в начальный момент времени, если граничные плоскости х= 0 и x=l (торцы стержня) поддерживаются при постоянной нулевой температуре.

В этом случае собственные значения определяются выражением

(99)

а собственные функции имеют вид

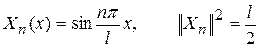. (100)

Следовательно, решение данной краевой задачи определяется формулой

, (101)

где

. (102)

2. При значении параметров краевые условия принимают вид

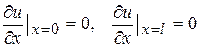. (103)

В этом случае краевая задача (84),(85), (103) описывает процесс выравнивания температуры в плоском слое (стержне), в котором в начальный момент времени задан температурный профиль 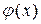, а граничные плоскости х= 0 и x=l (торцы стержня) идеально теплоизолированы.

Для этого случая

(104)

а собственные функции имеют вид

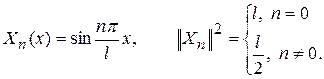(105)

Следовательно, решение данной краевой задачи определяется формулой

, (106)

где

. (107)

Необходимо отметить, что при t→∞ температура всех слоев выравнивается и стремиться к стационарному распределению

.

3. При значении параметров краевые условия принимают вид

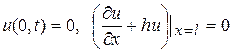. (108)

В этом случае смешанная краевая задача (84),(85), (108) описывает эволюцию температурного поля в плоском слое 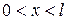тела, начальное распределение температуры в котором задано функцией 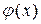, если на поверхности х= 0 поддерживается постоянная нулевая температура, а на другой поверхности x=l происходит конвективный теплообмен с окружающей средой, имеющей нулевую температуру.

Для этого случая

(109)

а собственные функции имеют вид

. (110)

Значения 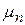являются действительными положительными корнями трансцендентного уравнения: .

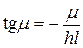Таким образом, решение смешанной краевой задачи определяется формулой

, (111)

где

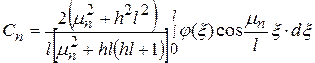. (112)

Дата добавления: 2014-10-22