
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решения краевой задачи для уравнения Лапласа внутри круга и вне его
|
|
|
|
Уравнением Лапласа описываются различные физические процессы и в каждой задаче искомое решение должно удовлетворять уравнению в некоторой области D, а также некоторому дополнительному условию на границе S этой области D.
В зависимости от вида граничного условия различают следующие основные виды граничных задач:
 - первая краевая задача или задача Дирихле;
- первая краевая задача или задача Дирихле;
 - вторая краевая задача или задача Неймана;
- вторая краевая задача или задача Неймана;
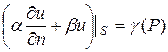 - третья краевая задача,
- третья краевая задача,
где 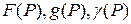 - определенные на поверхности S функции; Р – точка поверхности S;
- определенные на поверхности S функции; Р – точка поверхности S;  - внешняя нормаль к S;
- внешняя нормаль к S;  .
.
Краевые задачи могут быть внутренними или внешними. Они различаются в зависимости от того, в какой области внутренней или внешней относительно поверхности S ищется решение.
Внутренняя задача Дирихле формулируется следующим образом: Найти непрерывную в замкнутой области  функцию и (М), которая удовлетворяла бы в области D уравнению Лапласа и принимала бы на поверхности S заданные значения F(P). Математически это можно записать следующим образом:
функцию и (М), которая удовлетворяла бы в области D уравнению Лапласа и принимала бы на поверхности S заданные значения F(P). Математически это можно записать следующим образом:

Внутренняя задача Неймана формулируется так: найти внутри области D решение и (М) уравнения Лапласа
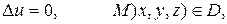
непрерывное в замкнутой области  и удовлетворяющее на поверхности S условию
и удовлетворяющее на поверхности S условию

Рассмотрим теперь краевые задачи для уравнения Лапласа внутри круга и вне его. Пусть существует область, представляющая собой круг радиуса R. Запишем двухмерное уравнение Лапласа в полярных координатах, полагая, что  , а
, а 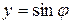
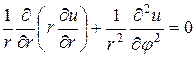 или
или  . (158)
. (158)
Для нахождения частных решений уравнения (158) используем метод Фурье и представим эти решения в виде
 (159)
(159)
После подстановки решения (159) в исходное уравнение (158) для каждой функции  и
и  получим два уравнения
получим два уравнения
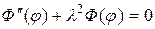 , (160)
, (160)
 . (161)
. (161)
Рассмотрим сначала уравнение (160) для функции  . Если
. Если  , то решение этого уравнения имеет вид
, то решение этого уравнения имеет вид
 . (162)
. (162)
Уравнение (161) в случае, когда  представляет собой уравнение Эйлера, которое можно привести к уравнению с постоянными коэффициентами путем замены
представляет собой уравнение Эйлера, которое можно привести к уравнению с постоянными коэффициентами путем замены  , тогда
, тогда
 .
.
Следовательно, уравнение (161) принимает вид
 .
.
Решение этого однородного линейного уравнения второго порядка имеет вид

и возвращаясь к переменной r, получим
 . (163)
. (163)
Если в уравнении (161)  , то это уравнение принимает вид
, то это уравнение принимает вид
 (164)
(164)
Это уравнение также является уравнением Эйлера, поэтому, производя замену  , приходим к уравнению
, приходим к уравнению
 ,
,
решение которого будет иметь вид
 ,
,
и возвращаясь к переменной r, получим
 . (165)
. (165)
решение уравнения (161) при  .
.
Таким образом, можно построить частные решения уравнения Лапласа в круге и вне его:
I. Исходя из выражений (159), (162), 163) и (165) можно утверждать, что частные решения уравнения Лапласа в круге можно записать в виде:
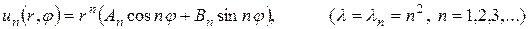
Эти решения ограничены при  и неограниченны на бесконечности.
и неограниченны на бесконечности.
Функция  как функция от
как функция от  является периодической функцией с периодом
является периодической функцией с периодом  , т.к. для однозначной функции величины
, т.к. для однозначной функции величины  и
и 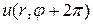 совпадают. Поэтому из равенства (158) следует, что коэффициент В в решении (162) равен нулю и
совпадают. Поэтому из равенства (158) следует, что коэффициент В в решении (162) равен нулю и 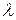 может принимать одно из значений 1,2,3,… (
может принимать одно из значений 1,2,3,… ( ). В решении (163) и (165) коэффициент D должен быть равным нулю, поскольку в противном случае функция
). В решении (163) и (165) коэффициент D должен быть равным нулю, поскольку в противном случае функция  имела бы разрыв в точке r = 0 и не была бы гармонической в круге. Следовательно, мы получили бесчисленное множество частных решений уравнения (158), непрерывных в круге, которые (несколько изменив обозначения) можно записать в виде
имела бы разрыв в точке r = 0 и не была бы гармонической в круге. Следовательно, мы получили бесчисленное множество частных решений уравнения (158), непрерывных в круге, которые (несколько изменив обозначения) можно записать в виде
 (166)
(166)
Используя принцип суперпозиции, а также вследствие линейности и однородности уравнения Лапласа можно утверждать, что сумма частных решений (166)
 (167)
(167)
будет являться решением уравнения (158).
Если поставлены краевые условия
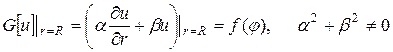 , (168)
, (168)
то решение краевой задачи можно записать в виде разложения (167), коэффициенты которого определяются из граничного условия (168). Решение можно получить немного иначе. Запишем решение задачи (158), (168) в виде
 (169)
(169)
 . Подставляя (169) в граничное условие (168), получаем
. Подставляя (169) в граничное условие (168), получаем
 (170)
(170)
Следовательно,  являются коэффициентами Фурье функции
являются коэффициентами Фурье функции  по системе тригонометрических функций
по системе тригонометрических функций  , которые можно вычислить по следующим формулам:
, которые можно вычислить по следующим формулам:
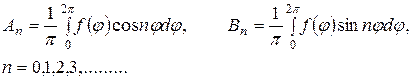 (171)
(171)
Выпишем отдельно решение первой, второй и третьей краевых задач для уравнения Лапласа в круге.
1. Задача Дирихле:  ,
,
 . (172)
. (172)
Подставляя коэффициенты  в (172) и меняя порядок суммирования и интегрирования, получим
в (172) и меняя порядок суммирования и интегрирования, получим
 .
.
Так как при  имеет место разложение
имеет место разложение
 ,
,
то решение можно записать в виде
 . (173)
. (173)
Эта формула Пуассона, которая при непрерывной функции  дает классическое решение задачи Дирихле в круге.
дает классическое решение задачи Дирихле в круге.
2. Задача Неймана:  ,
,
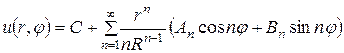 . (174)
. (174)
где С – произвольная постоянная.
Необходимо отметить, что решение задачи Неймана существует только при условии

и определяется с точностью до произвольной постоянной.
3. Третья краевая задача:
 ,
,
 (175)
(175)
Коэффициенты в решениях (172), (174), (175) определяются по формулам (171).
II. Рассмотрим теперь внешнюю краевую задачу для уравнения Лапласа
 ,
,
 ,
,
функция и регулярна на бесконечности, т.е. она имеет конечный предел при  .
.
Решение этой задачи можно записать в виде
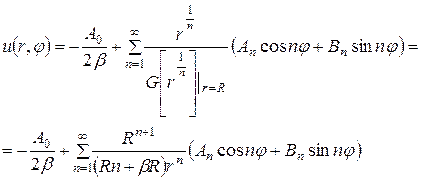 (176)
(176)
 . Коэффициенты
. Коэффициенты  определяются из граничного условия и вычисляются по формулам
определяются из граничного условия и вычисляются по формулам
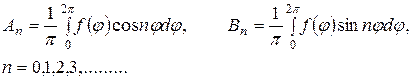 (177)
(177)
Выпишем отдельно решение первой, второй и третьей краевых задач для уравнения Лапласа вне круга.
1. Задача Дирихле:  ,
,
 . (178)
. (178)
2. Задача Неймана:  ,
,
 . (179)
. (179)
где С – произвольная постоянная.
Еще раз необходимо отметить, что решение задачи Неймана существует только при условии

и определяется с точностью до произвольной постоянной.
3. Третья краевая задача:
 ,
,
 . (180)
. (180)
Коэффициенты в решениях (178)-(180) являются коэффициентами Фурье функции  , и определяются по формулам (177).
, и определяются по формулам (177).
Пример 18. Найти решение уравнения Лапласа для внутренней части круга радиуса R, удовлетворяющее краевому условию
 . (18.1)
. (18.1)
▲ Здесь задана задача Дирихле, где правая часть граничного условия (18.1)  . Решение ищется в круге
. Решение ищется в круге  , значит выписывать решение будем по (172). Найдем в этой формуле коэффициенты
, значит выписывать решение будем по (172). Найдем в этой формуле коэффициенты 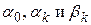 . Для этого подставим само решение (172) в левую часть граничного условия (18.1) при
. Для этого подставим само решение (172) в левую часть граничного условия (18.1) при 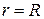 , а правую часть, т.е. функцию
, а правую часть, т.е. функцию  разложим в ряд Фурье по синусам и косинусам
разложим в ряд Фурье по синусам и косинусам
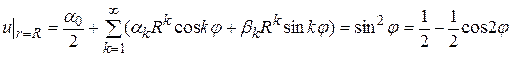 . (18.2)
. (18.2)
Теперь сравним коэффициенты при синусах и косинусах с одинаковыми аргументами и при свободном члене в левой и правой частях полученного равенства (18.2)

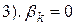 (при
(при  ), т.к. справа нет слагаемых с
), т.к. справа нет слагаемых с  ,
,
а также все остальные  (кроме
(кроме  ). Подставим ненулевые
). Подставим ненулевые  в решение (172) и получим ответ, т.е. найдем функцию
в решение (172) и получим ответ, т.е. найдем функцию 
 ▲
▲
Пример 19. Найти решение уравнения Лапласа во внешности круга радиуса R  , удовлетворяющее на границе условию Неймана
, удовлетворяющее на границе условию Неймана
 (19.1)
(19.1)
▲ Здесь дана задача Неймана, где правая часть граничного условия (19.1)  (уже разложена в ряд Фурье). Так как уравнение Лапласа надо решить вне круга
(уже разложена в ряд Фурье). Так как уравнение Лапласа надо решить вне круга  , то будем использовать формулу (178). Найдем в этой формуле коэффициенты
, то будем использовать формулу (178). Найдем в этой формуле коэффициенты  . Для этого подставим само решение (178) в левую часть граничного условия (19.1) при
. Для этого подставим само решение (178) в левую часть граничного условия (19.1) при 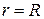 :
:
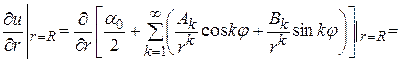
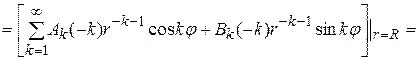
 (19.2)
(19.2)
Теперь сравним коэффициенты при синусах и косинусах с одинаковыми аргументами в левой и правой частях полученного равенства (19.2):

а все остальные 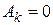 .
.

а все остальные  .
.
Подставим полученные ненулевые коэффициенты  в решение (178) и получим ответ, т.е. найдем функцию
в решение (178) и получим ответ, т.е. найдем функцию 
 ▲
▲
Задания для самостоятельной работы
Решить краевую задачу для уравнения Лапласа внутри круга  со следующими граничными условиями:
со следующими граничными условиями:
42.  .
.
43.  .
.
44.  .
.
45. 
46. 
Решить краевую задачу для уравнения Лапласа вне круга  со следующими граничными условиями:
со следующими граничными условиями:
47. 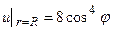 .
.
48. 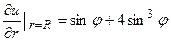 .
.
49.  .
.
50.  .
.
51.  .
.
Ответы на задания для самостоятельной работы
1.  .
.
2.  . 3.
. 3. .
.
4.  .
.
5.  .
.
6.  .
.
7.  .
.
8.  . 9.
. 9.  .
.
10.  . 11.
. 11.  .
.
12. 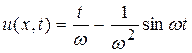 . 13.
. 13. 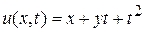 .
.
14.  .
.
15.  .
.
16.  .
.
17. 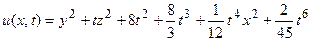 .
.
18.  .
.
19. 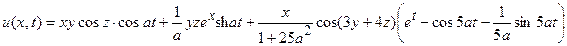 .
.
20.  .
.
21.  .
.
22.  .
.
23. 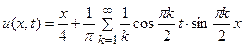 .
.
24. .
.
25.  .
.
26.  .
.
27. 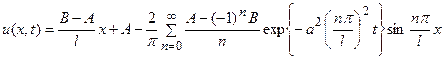 .
.
28.  .
.
29. 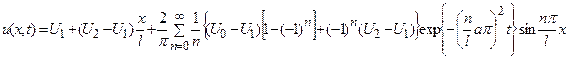 .
.
30.  . 31.
. 31.  .
.
32. . 33.
. 33.
34.  . 35.
. 35. .
.
36.  .
.
37.  .
.
38.  .
.
39. 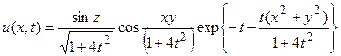 .
.
40.  .
.
41.  .
.
42. 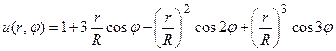 .
.
43.  .
.
44.  . 45.
. 45. .
.
46.  .
.
47. 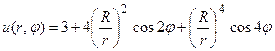 .
.
48.  . 49.
. 49. 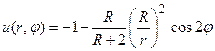 .
.
50.  . 51.
. 51.  .
.
ВНИМАНИЕ, КОНТРОЛЬНЫЕ РАБОТЫ ДОЛЖНЫ БЫТЬ НАПИСАНЫ ОТ РУКИ. В НАПЕЧАТАННОМ ВИДЕ РАБОТЫ ПРИНИМАТЬСЯ НЕ БУДУТ!
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 3278; Нарушение авторских прав?; Мы поможем в написании вашей работы!