
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение уравнения теплопроводности методом Тейлора
|
|
|
|
Задача Коши для уравнения теплопроводности
В первую очередь рассмотрим задачу Коши дляоднородного уравнения теплопроводности.
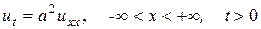 , (125)
, (125)
удовлетворяющее неоднородному начальному условию
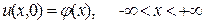 . (126)
. (126)
Начнем с того, что заменим переменные x и t на 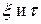 и введем в рассмотрение функцию
и введем в рассмотрение функцию  . Тогда функции
. Тогда функции 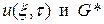 будут удовлетворять уравнениям
будут удовлетворять уравнениям

где  - функция Грина, определяемая формулой
- функция Грина, определяемая формулой
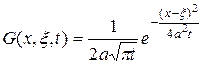 , (127)
, (127)
и обладающая свойствами
 (128)
(128)
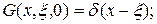 (129)
(129)
 ; (130)
; (130)
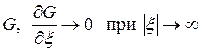 . (131)
. (131)
Умножив первое уравнение на G*, а второе на и и затем сложив полученные результаты, получим равенство
 . (132)
. (132)
После интегрирования по частям равенства (132) по 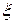 в пределах от -∞ до +∞ и по
в пределах от -∞ до +∞ и по 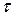 в пределах от 0 до t, получим
в пределах от 0 до t, получим
 . (133)
. (133)
Если предполагать, что функция 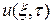 и ее производная
и ее производная  ограничены при
ограничены при 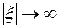 , то в силу свойств (131) интеграл в правой части (133) равен нулю. Следовательно, можно записать
, то в силу свойств (131) интеграл в правой части (133) равен нулю. Следовательно, можно записать
 . (134)
. (134)
Заменив в этом равенстве 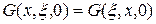 на
на  , а
, а 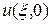 на
на  , получим соотношение
, получим соотношение
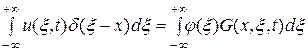
или
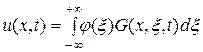 .
.
Отсюда, используя формулу (127) окончательно получим
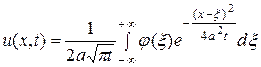 . (135)
. (135)
Формула (135) называется формулой Пуассона и определяет решение задачи Коши (125), (126) для однородного уравнения теплопроводности с неоднородным начальным условием.
Решение же задачи Коши для неоднородного уравнения теплопроводности
 , (136)
, (136)
удовлетворяющее неоднородному начальному условию
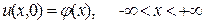 , (137)
, (137)
представляет собой сумму решений:
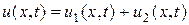 ,
,
где 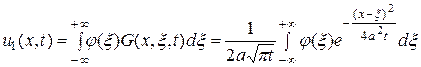 является решением задачи Коши для однородного уравнения теплопроводности.
является решением задачи Коши для однородного уравнения теплопроводности. 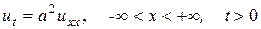 , удовлетворяющее неоднородному начальному условию
, удовлетворяющее неоднородному начальному условию 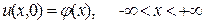 , а
, а  является решением
является решением 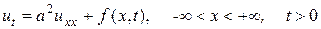 , удовлетворяющее однородному начальному условию
, удовлетворяющее однородному начальному условию 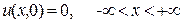 . Таким образом, решение задачи Коши (136), (137) определяется формулой
. Таким образом, решение задачи Коши (136), (137) определяется формулой
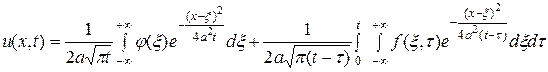 .(138)
.(138)
Пример 15. Найти решение уравнения
 (15.1)
(15.1)
для следующего распределения температуры стержня:
 (15.2)
(15.2)
▲ Стержень является бесконечным, поэтому решение можно записать, используя формулу (135)
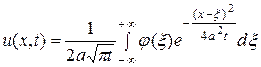 .
.
Так как  в интервале
в интервале  равна постоянной температуре
равна постоянной температуре  , а вне этого интервала температура равна нулю, то решение принимает вид
, а вне этого интервала температура равна нулю, то решение принимает вид
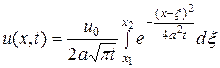 . (15.3)
. (15.3)
Полагая в (15.3) 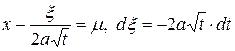 , получим
, получим
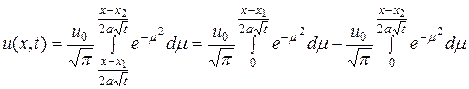 .
.
Поскольку
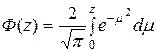
представляет собой интеграл вероятностей, то окончательное решение исходной задачи (13.1), (13.2) можно выразить формулой
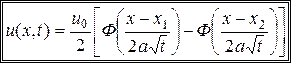 .▲
.▲
Задача Коши для уравнения теплопроводности имеет вид
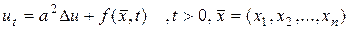 (139)
(139)
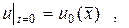 (140)
(140)
где 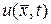 – неизвестная функция,
– неизвестная функция,  – заданы.
– заданы.
Разложим функцию 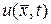 при любом фиксированном
при любом фиксированном 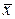 в ряд Тейлора по времени относительно точки t =0 (ряд Маклорена)
в ряд Тейлора по времени относительно точки t =0 (ряд Маклорена)
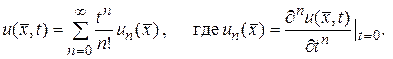
 (141)
(141)
Если найти коэффициенты  , то по формуле (141) получим решение. Заметим, что
, то по формуле (141) получим решение. Заметим, что 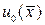 определяется из начального условия (140).
определяется из начального условия (140).
Разложим в ряд Маклорена функцию 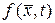 в правой части уравнения (139)
в правой части уравнения (139)
 (142)
(142)
Поскольку функция 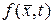 задана, то все
задана, то все 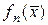 могут быть найдены.
могут быть найдены.
Выражения для частной производной 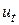 и оператора Лапласа
и оператора Лапласа 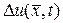 в уравнении (139), следуют из (141)
в уравнении (139), следуют из (141)
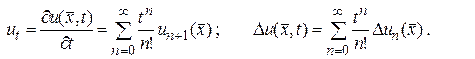 (143)
(143)
Подставим (142) и (143) в уравнение (139). В результате получим равенство
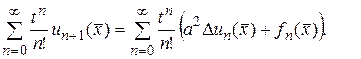
Это равенство равносильно соотношениям
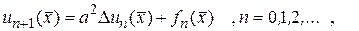 (144)
(144)
которые определяют коэффициенты 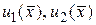 и так далее через
и так далее через 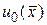 , заданную в начальном условии (140).
, заданную в начальном условии (140).
Таким образом, решение задачи Коши (139)–(140) выражается формулой:
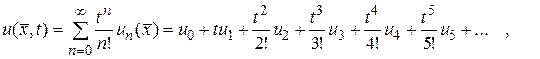 (145)
(145)
где 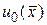 задана в (140), а остальные
задана в (140), а остальные  находятся по (144)
находятся по (144)
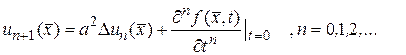 (146)
(146)
Пример 16. Найти решение уравнения
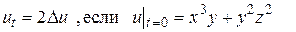
▲ Здесь 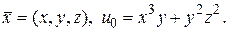 Так как
Так как  и
и  , то по (146)
, то по (146) 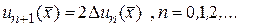 Отсюда находим
Отсюда находим
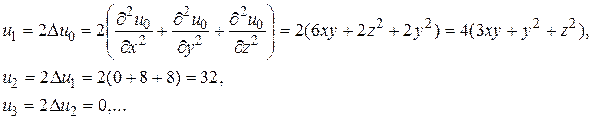
То есть, все остальные 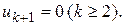
Подставляем полученные 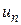 в решение (145)
в решение (145)
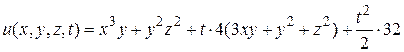
или
 ▲
▲
Пример 17. Найти решение уравнения

▲ Здесь 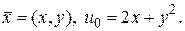 Так как
Так как 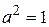 и
и  , то по (146)
, то по (146)
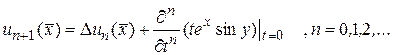
Найдем 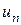 по этой формуле
по этой формуле

И так далее, все остальные 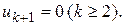
Подставляем полученные 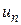 в решение (145)
в решение (145)

или
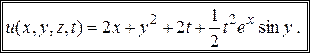 ▲
▲
Задания для самостоятельной работы
Решить задачи Коши для уравнения теплопроводности
30. 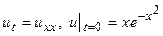 . 31.
. 31.  .
.
32.  . 33.
. 33. 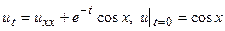 .
.
34.  . 35.
. 35. 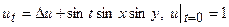 .
.
36.  . 37.
. 37.  .
.
38. 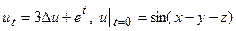 . 39.
. 39.  .
.
40. 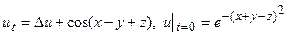 .
.
41.  .
.
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 1069; Нарушение авторских прав?; Мы поможем в написании вашей работы!