Рассмотрим задачу для неоднородного уравнения теплопроводности

Неоднородное уравнение теплопроводности

, (113)

с начальными условиями

, (114)

и граничными условиями

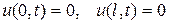. (115)

Решение этой задачи будем искать в виде ряда Фурье по системе собственных функций (94)

,

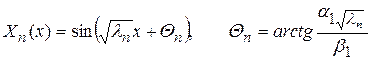т.е. в форме разложения

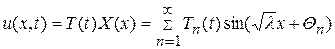, (116)

считая при этом t параметром.

Пусть функции f(x,t) является непрерывной и имеет кусочно-непрерывную производную 1-го порядка по х и при всех t >0 выполняются условия

.

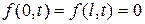Предположим теперь, что функции f(x,t) и 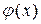можно разложить в ряд Фурье по синусам

, (117)

где

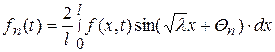(118)

и

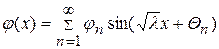, (119)

где

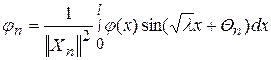. (120)

Подставим (116) в уравнение (113) и с учетом (117), получим

.

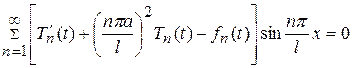Это равенство выполняется тогда, когда

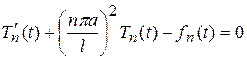, (121)

или, если 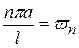, то это уравнение (121) можно записать в виде

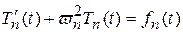. (122)

Пользуясь начальным условием (114) с учетом (116), (117) и (119) получаем, что

,

откуда

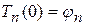. (123)

Таким образом, для нахождения искомой функции 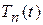приходим к задаче Коши (122), (123) для обыкновенного неоднородного дифференциального уравнения первого порядка. Пользуясь формулой Эйлера можно записать общее решение уравнения (122)

,

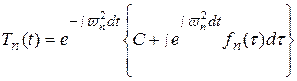а с учетом (123) решение задачи Коши

.

Следовательно, когда мы подставим значение этой функции в выражение (116), в итоге получим решение исходной задачи

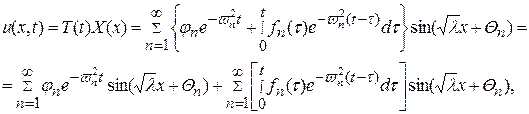(124)

где функции f(x,t) и 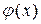определены формулами (118) и (120).

Пример 14. Найти решение неоднородного уравнения параболического типа

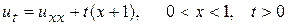(14.1)

при начальном условии

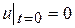(14.2)

и граничных условиях

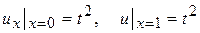. (14.3)

▲ Подберем сначала такую функцию v, чтобы удовлетворяла граничным условиям (14.3). Пусть, например, v = xt ². Тогда

Следовательно, функция определяемая как

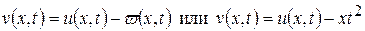(14.4)

удовлетворяет уравнению

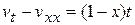(14.5)

однородным граничным условиям

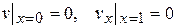(14.6)

и нулевым начальным условиям

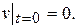. (14.7)

Применяя метод Фурье для решения однородного уравнения

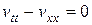
при условиях (14.6), (14.7), положим

.

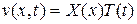Приходим к следующей задаче Штурма-Лиувилля:

, .

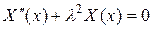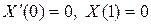Решая эту задачу, находим собственные значения

и соответствующие им собственные функции

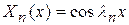. (14.8)

Решение задачи (14.5)-(14.7) ищем в виде ряда

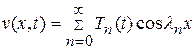, (14.9)

где

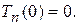(14.10)

Подставив 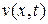из (14.9) в (14.5) получим

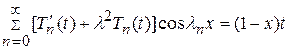. (14.11)

Для нахождения функции T_n(t) разложим функцию (1- х) в ряд Фурье по системе функций (14.8) на интервале (0,1):

. (14.12)

Так как

,

и из (14.11) и (14.12) получаем уравнение

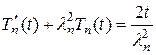, (14.13)

которое является обыкновенным неоднородным линейным дифференциальным уравнением первого порядка. Его общее решение найдем по формуле Эйлера

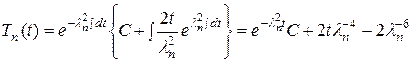
а с учетом условия (14.10), найдем решение задачи Коши

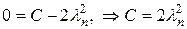
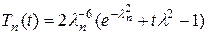. (14.14)

Из (14.4), (14.9) и (14.14) находим решение исходной задачи (14.1)- (14.3)

.▲

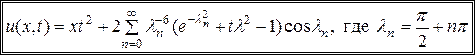Задания для самостоятельной работы

Решить начально-краевые задачи

25. .

26. .

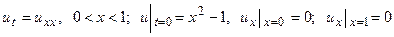27. .

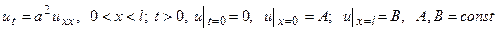28. .

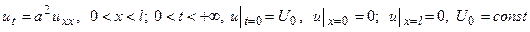29. .

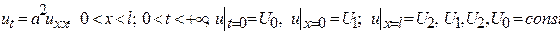Дата добавления: 2014-10-22