Средняя арифметическая

Самым распространенным видом средней, применяемой в социально-экономическом анализе, является средняя арифметическая.

Средняя арифметическая простая:

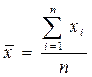,где

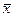
	– средняя величина,
x	– индивидуальные значения признака отдельных единиц совокупности,
n	– численность совокупности.

Простая средняя арифметическая используется в расчете популярного фондового индекса Доу-Джонса, для определения среднего остатка оборотных средств по балансу, среднегодовой численности населения и др.

Средняя арифметическая взвешенная:

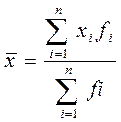, где

f – частота.

Данная формула широко применяется в расчетах экономических показателей. Например, надо определить среднюю заработную плату работника АО, имея данные по отдельным филиалам АО (табл. 4.1.):

Таблица 4.1

Сведения о заработной плате

Филиалы АО	Заработная плата работника, в гривнах	Численность работников

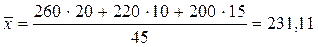грн.

Средняя арифметическая величина может быть дроб­ным числом, если даже индивидуальные значения признака могут принимать только целые значения (дискретный признак). Ничего «предосудительного» для метода средних в этом не заключено; из сущности средней не вытекает, что она обязана быть реальным значением признака, которое могло бы встретиться у какой-либо единицы совокупности.

Если при группировке значения осредняемого признака зада­ны интервалами, то при расчете средней арифметической вели­чины в качестве значения признака в группах принимают сере­дины этих интервалов, т.е. исходят из гипотезы о равномерном распределении единиц совокупности по интервалу значений при­знака. Для открытых интервалов в первой и последней группе, если таковые есть, значения признака надо определить эксперт­ным путем исходя из сущности, свойств признака и совокупности.

Свойства арифметической средней величины

Знание некоторых математических свойств средней арифме­тической полезно как при ее использовании, так и при ее расчете.

1. Сумма отклонений индивидуальных значений признака от его среднего значения равна нулю.

Доказательство:

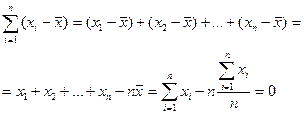
Примечание. Для средней взвешенной сумма взвешенных от­клонений равна нулю.

2. Если каждое индивидуальное значение признака умножить или разделить на постоянное число, то и средняя увеличится или умень­шится во столько же раз.

Доказательство:

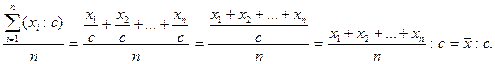
Вследствие этого свойства индивидуальные значения признака можно сократить в с раз, произвести расчет средней и результат умножить на с.

3. Если к каждому индивидуальному значению признака приба­вить или из каждого значения вычесть постоянное число, то сред­няя величина возрастет или уменьшится на это же число.

Доказательство:

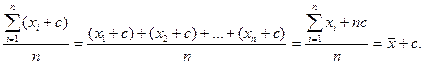
Это свойство полезно использовать при расчете средней величи­ны из многозначных и слабоварьирующих значений признака.

4. Если веса средней взвешенной умножить или разделить на постоянное число, средняя величина не изменится.

Доказательство:

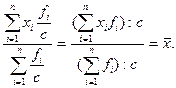
Используя это свойство, при расчетах следует сокращать веса на их общий сомножитель либо выражать многозначные числа весов в более крупных единицах измерения.

5. Сумма квадратов отклонений индивидуальных значений при­знака от средней арифметической меньше, чем от любого другого числа.

Доказательство. Составим сумму квадратов отклонений от переменной а:

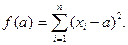
Чтобы найти экстремум этой функции, нужно ее производную по а приравнять нулю:

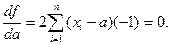
Отсюда имеем:

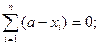
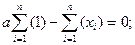
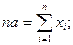
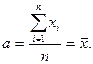
Таким образом, экстремум суммы квадратов отклонений дости­гается при 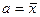. Так как логически ясно, что максимума функция не может иметь, этот экстремум является минимумом.

Дата добавления: 2014-10-22