Скользящая средняя

Средняя хронологическая

Где

Õ(x^f) – произведение

f – продолжительность отрезков времени.

Например: Первые два года фирма увеличила выручку от реализации на 10% или в 1,1 раза ежегодно, за следующие 3 года она увеличивала ежегодно на 20% или в 1,2раза. Чему равен среднегодовой темп роста выручки от реализации за весь период работы фирмы?

или 116%

Средняя хронологическая вычисляется по формуле:

, где

n- число дат

– уровни ряда

Если значение признака приводится на конкретную дату, то для расчета среднего уровня ряда применяется средняя хронологическая. Например, имеются остатки незавершенного производства по фирме: на 1.01-200 тыс. грн., 1.02-180 тыс. грн., 1.03-160 тыс. грн., 1.04-190 тыс. грн. Определить средний остаток незавершенного производства за первый квартал.

тыс. грн.

Суть расчета средней скользящей состоит в том, что по эмпирическим данным вычисляют скользящие средние, которые получают из сумм показателей, последовательно сдвигающихся на одну дату по ряду. Затем подвижные суммы следует разделить на число дат, принятых за период сглаживания. Таким образом, получаем скользящую среднюю.

Произведем сглаживание данных о курсе акций (цифры условные) при помощи трехдневной средней. Найдем среднее значение для первых трех уровней:

(80+72+99)/3=84 и отнесем его ко второму дню. Затем отбросим первый член ряда, прибавим четвертый день и рассчитаем для третьего дня: (77+99+120)/3=97 и т.д. Получим следующие средние скользящие (табл. 4.4):

Таблица 4.4

Определение средней скользящей

День	Цена акции, грн.	Скользящая средняя
		-
		-

7. Структурные средние (мода и медиана)

К структурным средним относятся мода и медиана. Мода (М₀) – наиболее часто встречающееся значения признака в совокупности. Например: 2, 4, 3, 3, 3, 3, 1, 5. Мода – 3. Обычно встречаются ряды с одним модальным значением признака. В противном случае ряд называется бимодальным или мультимодальным.

В интервальном вариационном ряду модальным интервалом считается интервал с наибольшей частотой. В этом случае для вычисления моды используется следующая формула:

где: - нижняя граница модального интервала;

- частота в модальном интервале;

- частота в интервале, предшествующем модальному;

- частота в интервале, следующим за модальным;

i – величина интервала.

Медиана (М_е) – середина ранжированного статистического ряда. Медиана делит ряд на две равные части. Вначале определяют порядковый номер медианы:

N_me=(n+1)/2,

где n – объем ряда (число единиц в ряду).

Если ряд состоит из четного числа членов, то медиана определяется как полусумма двух срединых вариант. Так, дан ряд 10, 20, 30, 40, 50,..., 80

N_me=(8+1)/2=4,5, М_е=(40+50)/2=45.

В интервальном вариационном ряду для нахождения медианы применяется формула:

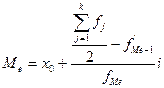
где: Ме – медиана

- нижняя граница интервала, в котором находится медиана;

- накопленная частота в интервале, предшествующем медианному;

- частота в медианном интервале;

i – величина интервала;

k – число групп.

В дискретном вариационном ряду медианой считается значение признака в той группе, в которой накопленная частота превышает половину числа единиц совокупности.

Аналогично медиане вычисляются значения признака, делящие совокупность на 4 равные части (по числу единиц). Эти величины называют квартилями и обозначают буквой Q со значком номера квартиля. 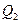совпадает с медианой. Первый и третий квартили рассчитываются по следующим формулам:

Значения признака, делящие ряд на 5 равных частей, называются квинтилями, на десять – децилями, на 100 – перцентилями.

Дата добавления: 2014-10-22