Дисперсия и среднее квадратическое отклонение. Тема 5. Показатели вариации

Размах вариации

Тема 5. Показатели вариации

1. Размах вариации

2. Дисперсия и среднее квадратическое отклонение

3. Коэффициенты вариации и дифференциации

4. Моменты распределения и показатели его формы

5. Виды и взаимосвязь дисперсий

Вариацией признака называется его изменение у единиц совокупности. Вариация порождается комплексом разнообразных условий, фактов, воздействующих на элементы совокупности. Изучение вариации имеет большое практическое и научное значение. Оно осуществляется при помощи показателей вариации.

Размах вариации – разность между максимальным и минимальным значением признака изучаемой совокупности.

W=X_max-X_min

где: W – размах вариации,

X_max – наибольшее значение признака,

X_min – наименьшее значение признака.

Величина размаха вариации вычисляется по крайним точкам ряда, которые в наибольшей степени подвержены случайным изменениям. Поэтому принято считать более надежным показателем инквартильный размах. Он вычисляется как разность между третьим и первым квартилем.

R=Q₃-Q₁

где: Q₁- первый квартиль,

Q₃ – третий квартиль.

В качестве показателя силы вариации используют среднее линейное отклонение:

.

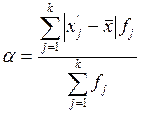Показатель среднего квадратического отклонения рассчитывается по следующей формуле:

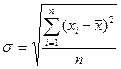. Для дискретного ряда

. Для интервального ряда

Квадрат среднего квадратичного отклонения называется дисперсией.

Дисперсия – средний квадрат отклонений индивидуальных значений признака от их средней величины.

, где

σ²(сигма)	– дисперсия;
хi	– значение признака отдельных единиц совокупности;
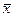
	– среднее значение всех единиц совокупности;
n	– численность совокупности.

Для вариационного ряда дисперсия вычисляется по следующей формуле:

Дисперсия признака равна разности между средним квадратом значений признака и квадратом их средней, т.е.

,

а для вариационного ряда

Доказательство:

заменим и разделим все слагаемые на n:

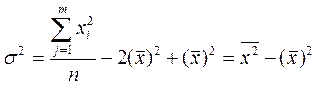
Размах вариации, среднее квадратическое отклонение являются именованными величинами. Чем меньше эти показатели, тем совокупность более однородна, тем более типичной будет средняя величина.

Дисперсия альтернативного признака вычисляется по формуле:

s²=pq,

где: р – доля единиц обладающих данным признаком,

q – доля единиц, не обладающих данным признаком.

q=1-p.

Среднее квадратическое отклонение альтернативного признака:

Дата добавления: 2014-10-22