Ошибки выборки

Виды выборки. Способы отбора.

Если используются результаты эксперимента, рассматриваемого как некоторая выборка из бесконечно большого числа экспериментов.

Поскольку выборочная совокупность не абсолютно точно отражает состав генеральной совокупности, то и статистические оценки выборочной совокупности не абсолютно точно совпадают с оценками генеральной совокупности. Отличие состоит в ошибке наблюдения и в ошибке выборки:

выборочная оценка = генеральный параметр ± ошибка наблюдения ± ошибка выборки.

Для того, чтобы по выборочной совокупности делать какие-то выводы о генеральной совокупности, выборочная совокупность должна быть репрезентативной, т.е. достаточно точно отражать свойства генеральной совокупности. Репрезентативность выборки может быть обеспечена при соблюдении объективности отбора данных. Возможны три способа отбора:

Ø случайный;

Ø по определенной схеме;

Ø сочетание первого и второго способа.

Виды выборки:

Ø типическая (расслоенная, стратифицированная, районированная) – выборка производится из генеральной совокупности, предварительно разделенной на типы (слои, страты);

Ø серийная (гнездовая) – единицей отбора является не единица наблюдения, а серия (гнездо) единиц совокупности;

Ø повторная или бесповторная;

Ø многоступенчатая, которая используется при изучении социально-экономических объектов сложной структуры, когда на каждой ступени используются разные единицы отбора – от более крупных до единицы наблюдения на последней ступени;

Ø многофазовая, включающая определенное количество, каждая из которых имеет программу наблюдения со своей степенью подробности.

От случайной выборки следует отличать квотный отбор, когда выборка конструируется из единиц определенных категорий (квот). Выборка может быть нерепрезентативной, даже если она формируется в соответствии с известными пропорциями генеральной совокупности, но отбор производится без определенной схемы.

Ошибка выборки представляет собой разность между значением показателя, полученного по выборке, и генеральным параметром. Принято среднюю, относительную величину и дисперсию в генеральной совокупности обозначать соответственно как m, p, s², а в выборочной совокупности - , r, s².

Тогда ошибка репрезентативности выборочной средней равна:

,

выборочной относительной величины:

,

дисперсии:

.

Если представить, что было произведено бесконечно большое число выборок равного объема из одной и той же генеральной совокупности, то показатели этих выборок образовали бы ряд возможных значений: выборочных средних величин, дисперсии, относительных величин. Для каждой отдельной выборки характерна своя ошибка репрезентативности. Следовательно, можно было бы построить ряды распределения выборок по величине ошибки репрезентативности для каждого показателя. В таких распределениях улавливается тенденция в концентрации ошибок около центрального значения. Число выборок с той или иной величиной ошибки репрезентативности может быть симметрично или ассиметрично относительно этого центрального значения. При бесконечно большом числе выборок получается кривая частот, которая называется кривой выборочного распределения. Свойства таких распределений используются для получения статистических заключений, установления вероятности той или иной величины ошибки репрезентативности.

Рассмотрим выборочное распределение средней величины. С увеличением числа выборок средняя всех выборок будет приближаться к генеральной средней, т.е. , а .

Средняя ошибка выборочной средней при повторном отборе определяется по формуле:

;

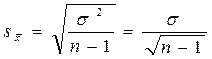При бесповторном отборе:

Из формулы следует, что средняя ошибка выборки тем больше, чем больше вариация в генеральной совокупности, и тем меньше, чем больше объем выборки.

Если значения n достаточно велики (n>100), то приведенные формулы средней ошибки выборочной средней можно использовать в следующем виде:

При повторном отборе:

;

При бесповторном отборе:

Ошибка конкретной выборки может принимать различные значения, но отношение ее к средней ошибке практически не превышает ±3, если величина n достаточно большая (>100).

Средняя ошибка выборочной средней показывает возможные отклонения характеристик выборочной совокупности от характеристик генеральной совокупности. В практическом смысле имеет значение нахождение предельной ошибки выборки. Зная среднюю ошибку выборки, можно найти границы, за которые не выйдет величина конкретной ошибки выборки. Однако это можно утверждать только с определенной степенью вероятности.

Доверительный уровень вероятности – это такой уровень вероятности, который устанавливают при определении границ, в которых находятся параметры генеральной совокупности.

Чаще всего принимают доверительную вероятность равной 0,95; 0,954; 0,997 или 0,999. Доверительный уровень вероятности 0,95 означает, что толь­ко в 5 случаях из 100 ошибка может выйти за установленные гра­ницы; вероятности 0,954 - в 46 случаях из 1000, при 0,997 - в 3 случаях, а при 0,999 - в 1 случае из 1000.

Уровень значимости (существенности) – это относительное количество ошибочных выводов в общем количестве выводов. Уровень значимости дополняет надежный уровень вероятности до 1.

Предельная ошибка выборки – это такая ошибка выборки, которая исчислена с заданным уровнем надежной вероятности.

Отношение ошибки конкретной выборки к средней ошибке выборочной средней называется нормированным отклонением и обозначается как t:

.

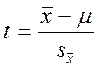В статистической литературе нормированное отклонение еще называется коэффициентом надежности или коэффициентом кратности.

Предельная ошибка выборки определяется по формуле:

.

С учетом приведенных формул:

При повторном отборе:

;

При бесповторном отборе:

В этом случае искомый надежный интервал для оценки генеральной средней по выборочной средней определяется по формуле:

Вероятность отклонения выборочных средних от генеральной средней при бесконечно большом числе наблюдений (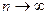) определяется законом нормального распределения Лапласа-Гаусса:

.

где:- плотность вероятности;

- среднее квадратичное отклонение значений переменной х от средней в генеральной совокупности.

Так как средняя нормированных отклонений t=0, дисперсия , т.е. 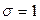, то выражение уравнения Лапласа-Гаусса может быть записано в следующем виде:

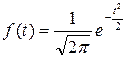
Это уравнение называется стандартным уравнением нормальной кривой. График кривой нормального распределения вероятностей имеет вид:

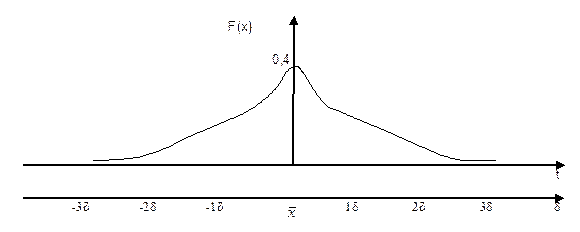
Площадь, ограниченная кривой и всей осью абсцисс равна 1.

Ординаты на графике соответствуют вероятности при том или ином значении t. Чтобы определить вероятность значений в некотором интервале от t₁ до t₂, следует найти отношение между частью площади кривой, заключенной между t₁ и t_{2 ,} ко всей площади кривой.

Уравнение Лапласа - Гаусса предполагает непрерывное изме­нение t и неограниченное возрастание n. Поэтому площадь нормаль­ной кривой, заключенную между ординатами t₁ и t₂ определяют, интегрируя функцию ().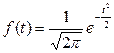

Имеются таблицы, которые содержат значения вероятностей для нормированных отклонений t или для интервалов от t₁ до t₂. Эти таблицы содержит пропорциональные доли пло­щадей, заключенных между ординатами, соответствующими ± t. Зная нормированное отклонение t, можно определить вероятность или на основе определенной вероятности установить величину t.

На пересечении строк и граф таблицы находится значение веро­ятности F(t), соответствующее данному значению t. Для краткости записи в таблице приводятся только десятичные знаки вероятности, следовательно, к табличному значению F(t) надо приписывать ноль целых.

При определении нормированного отклонения t по табли­це «Значение интеграла вероятностей» необходимо при­нять определенный уровень вероятности суждения о точности дан­ной выборки, для чего задаются уровнем доверительной вероятности.

Наиболее часто используют следующие значения нормированного отклонения и соответствующие им вероятности:

t	1,00	1,96	2,00	2,58	3,00
Ф(t)	0,6827	0,9500	0,9545	0,9901	0,9973

Относительная ошибка выборки определяется по формуле:

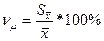В случае типического отбора всю генеральную совокупность разделяют на группы по изучаемому признаку, а затем из каждой группы случайным образом отбирают необходимое количество единиц. При этом необходимо обеспечить принцип пропорционального представительства каждой группы. Для этого используют показатель численности, или дисперсий, или средних квадратичных отклонений. Это дает возможность устранить межгрупповую дисперсию. Поэтому ошибка выборки определяется только средней из групповых дисперсий, которая меньше от общей дисперсии на величину межгрупповой дисперсии. Ее называют остаточной дисперсией.

Тогда средняя ошибка при типическом отборе определяется по следующим формулам:

При повторном отборе:

;

При бесповторном отборе:

Суть серийного отбора заключается в том, что отбираются не отдельные единицы совокупности, а серии таких единиц. При этом общее число серий рассматривают как численность генеральной совокупности, а количество отобранных серий как объем выборочной совокупности.

При серийном отборе устраняется влияние внутригрупповой вариации, поэтому при расчете ошибки выборки используют только вариацию между сериями.

4. Задачи, решаемые при применении выборочного метода

При применении выборочного метода возникает три основные задачи:

Ø определение возможного предела ошибок репрезентативности, гарантированного с заданной вероятностью;

Ø определение объемов выборки для получения требуемой точности результатов с заданной вероятностью;

Ø определение вероятности того, что ошибка выборки не превысит допустимой погрешности.

Дата добавления: 2014-10-22