Определение возможного предела ошибок репрезентативности, гарантированного с заданной вероятностью.

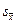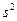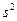Чтобы вычислить ошибку выборки при принятой доверительной вероятности, нужно рассчитать величину средней ошибки . Фор­мула для ее определения включает дисперсию признака в ге­неральной совокупности , которая, как правило, неизвестна. Мо­жет быть определена только выборочная дисперсия . Доказано, что соотношение между и определяется следующим равен­ством:

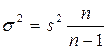
Если n велико, то сомножитель и можно принять выборочную дисперсию в качестве оценки величины генеральной дисперсии. Подставив предыдущее выражение в формулу средней ошибки выборочной средней, получим:

или

Соответственно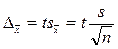

Пример. Для определения скорости расчетов с кре­диторами предприятий одного треста была проведена случайная выборка 50 платежных документов, по которым средний срок пере­числения денег оказался равен 28,2 дня со стандартным отклонени­ем 5,4 дня. Определим средний срок прохождения всех платежей в течение данного года с доверительной вероятностью F(t) = 0,95. Тогда по таблице значения интеграла вероятности t = 1,96; скорректированная дисперсия:

.

Средняя ошибка выборки:

Отклонение выборочной средней от генеральной с вероятностью 0,95 составит дня.

называется доверительной ошибкой выборки или предельной ошибкой выборки. Рассчитав величину , можно записать следующее неравенство:

28,2-1,5 £ £ 28,2+1,5

26,7 дня £ £ 29,7 дня

Таким образом, с вероятностью 0,95 можно утверждать, что средняя продолжительность расчетов предприятия данного треста с кредиторами составляет не менее 26,7 дня и не более 29,7 дня.

Ошибка для альтернативного признака (или для выборочной относительной величины, или для доли) определяется аналогично. Дисперсия относительной величины по данным выборки:

Средняя ошибка выборочной доли:

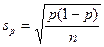
Предельная ошибка выборочной доли с принятой доверительной вероятностью имеет вид:

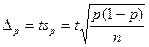
Пример. По данным выборочного изучения 100 платежных документов предприятия одного треста оказалось, что в 6 случаях сроки расчетов с кредиторами были превышены. С вероятностью 0,954 требуется установить доверительный интервал доли платежных документов треста без нарушения сроков:

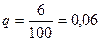или 6%, p=0,94

Генеральная доля платежных документов 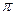, не выходящих за установленные сроки, с вероятностью 0,954 находится в интервале:

0,892£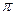£0,988 или 89,2%£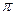£98,8%

Дата добавления: 2014-10-22