Оценка существенности различия средних

Для оценки существенности различия двух средних предназначен критерий t-Стьюдента, исчисляемый по формуле:

t_расч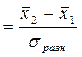, где

tрасч	– фактическое значение критерия t-Стьюдента,
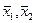
	–средние двух совокупностей,
sразн	– показатель колеблемости разности.

Показатель колеблемости разности может быть исчислен так:

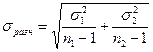, где

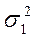
	– дисперсия признака в первой совокупности,
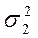
	– дисперсия признака во второй совокупности,
n1, n2	– объем совокупностей,
(n1-1), (n2-1)	– число степеней свободы

Если объемы совокупности велики, то приведенную формулу упрощают, т.е. в знаменателях дробей ставят просто n₁ и n₂. Исчисленное с помощью формулы фактическое значение критерия – t_расч. сравнивают с его критическим значением – t_кр. Если совокупность большого объема, то величина t_кр подчиняется закону нормального распределения и берется из таблиц интегральной функции нормального распределения F(t) или функции Лапласа Ф(t). Если расчеты ведутся по малой совокупности (n<30), то величина t_кр. подчиняется распределению Стьюдента и ее критическое значение берется из таблиц S(t)-распределения.

Если в ходе сравнения окажется, что t_расч£t_кр, то нулевую гипотезу считают не противоречащей данным наблюдения. При t_расч>t_кр нулевую гипотезу отвергают в пользу одной из альтернативных гипотез.

Рассмотрим расчет показателей вариации по следующим ее данным об успеваемости в двух группах студентов (табл. 4.4):

Таблица 4.4

Успеваемость студентов

Группы по полу	Число студентов в группе	Успеваемость отдельных студентов в баллах
Юноши Девушки		5; 5; 4,6; 4,5; 3,2; 3 4,2; 4,1; 4; 4; 3,9; 3,8

В какой группе успеваемость выше; являются ли различия в средней успеваемости двух групп студентов существенными?

	Юноши	Девушки
W	2,0	0,4
s^2	0,6617	0,0167
s	0,813	0,129
V	19,4%	3,2%

; ;

; .

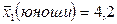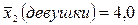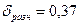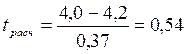t_кр=2,57 при числе степеней свободы (6-1=5) при 5%-ом уровне значимости.

Так как t_расч<t_кр (0,54<2,57), то различия в средней успеваемости двух групп студентов не существенны.

Дата добавления: 2014-10-22