Расчет уровня сезонности потребления воды населением

Сезонные колебания

Сезонными называют периодические колебания, возникающие под влиянием смены времени года. Поскольку интервальные уровни зависят от длительности интер­валов времени, а длина месяцев не равная, точнее проводить анализ сезонных колебаний не по фактическим месячным уровням, а по уровням, пересчитанным на равную (30-дневную) длительность всех месяцев или среднесуточным. Если изучаются сезонные колебания за отдельный год, то обычно тренд не принимается во внимание, и отклонения месячных (30-дневных) уровней, исчисляются от сред­немесячного уровня за год. Кроме рассмотренных показателей ко­леблемости для характеристики сезонных колебаний важное значе­ние имеет форма сезонной «волны», изучаемая с помощью относи­тельных показателей - отношений месячных уровней к среднеме­сячному (так называемый «индекс сезонности»). Изучать сезонные колебания следует за несколько лет, чтобы сгладить слу­чайные колебания и точнее измерить сезонные.

Рассмотрим сезон­ность потребления воды населением, соответствующие расчеты которой приведены в табл. 8.11.

Таблица 8.11.

	Среднесуточное потребление воды, тыс. куб. м.	В % к среднемесячному показателю	Отклонения от средней	Квадрат отклонения от средней
Месяц
			в среднем за 3 года
Январь	80,3	89,5	56,3	75,4	109,24	6,37	40,61
Февраль	85,3	96,4	59,4	80,3	116,43	11,34	128,54
Март	77,3	82,1	54,6	71,3	103,38	2,33	5,45
Апрель	75,3	86,4	56,0	72,6	105,17	3,57	12,73
Май	72,7	66,2	57,9	65,6	95,08	-3,40	11,54
Июнь	72,6	74,1	57,4	68,0	98,63	-0,95	0,90
Июль	73,5	60,8	54,1	62,8	91,04	-6,18	38,18
Август	73,1	61,6	54,2	63,0	91,25	-6,04	36,43
Сентябрь	82,0	66,5	55,4	68,0	98,52	-1,02	1,04
Октябрь	82,9	59,2	53,2	65,1	94,36	-3,89	15,15
Ноябрь	92,8	59,9	54,9	69,2	100,30	0,21	0,04
Декабрь	90,4	56,5	53,1	66,6	96,60	-2,35	5,51
Средняя	79,9	71,6	55,5	69,0	100,00	-	296,14

По данным табл. 8.11 потребление воды возрастает в зимние месяцы. Среднее квадратичное отклонение составляет 4,97. Коэффициент колеблемости равен 7,2% (4,97/69,0), что позволяет сделать выводы о достаточно слабой сезонной колеблемости потребления воды населением.

8. Прогнозирование на основе тренда и колеблемости

Методика ста­тистического прогноза по тренду и колеблемости основана на том предположении, что основные факторы, влияющие на формирование того или иного тренда и колеблемости, остаются постоянными на протяжении как самого динамического ряда, так и прогнозируемого периода. В этом случае говорят об экстрапо­ляции, под которой понимают получение представлений о буду­щем на основе информации, относящейся к прошлому и настоящему. Период экстраполяции не должен превышать одной трети исходного динамического ряда. Прогнозные значения динамического ряда, рассчитанные на основе некоторого уравнения тренда, называются теоретическими значениями ряда (в отличие от фактических значений исходного ряда). Период времени, на который делается прогноз, принято называть периодом упреждения.

Существует два принципиально различных класса моделей, ориентированных на использование тренда и колеблемости. Модели первого класса предполагают, что тренд и колеблемость между собой никаким образом не связаны, то есть изменения тренда и изменения колеблемости происходят независимо друг от друга. Модели второго класса предполагают взаимное влияние тренда и колеблемости.

При прогнозировании в данном случае рассматриваются модели первого класса, а потому каждое трендовое значение представляет собой сумму трендового значения по экспоненциальному тренду и трендового значения по колеблемости. Для этого необходимо рассчитать параметры уравнения колеблемости, чего вычисляются отклонения фактических значений динамического ряда от трендовых значений.

Если выявлены долгопериодические циклические колебания, то аналитическое сглаживание ряда отклонений фактический значений от тренда производят с помощью ряда Фурье. В этом случае уравнение колеблемости выглядит следующим образом:

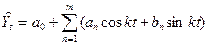
где: k – номер гармоники;

t – период времени, выраженный в радианах или градусах и представляющий собой последовательные промежутки времени, для которых построен динамический ряд. Начальное значение t принимается равным нулю. Шаг, с которым изменяется t рассчитывается по формуле:

,

где l - период колебаний, определенный ранее. К примеру, если обнаружены долгопериодические циклические колебания с периодом, равным одному году (12 месяцев), то шаг, с которым изменяется t будет равен .

Синусоиды, описываемые рядом Фурье, представляют собой гармоники различного порядка. Их наложение и позволяет составить суммарное уравнение колеблемости. При этом используется различное количество гармоник, однако практический опыт показывает, что их количество редко превышает 10 гармоники. Выбор количества гармоник проводят на основе анализа полученных данных. Для одной гармоники уравнение Фурье принимает вид:

Для двух гармоник:

Для трех гармоник:

и т.д.

Параметры уравнения Фурье вычисляются по следующим формулам:

Параметры уравнения колеблемости вычисляют для первых 10 гармоник. Оптимальное число гармоник находят по наименьшему значению квадрата отклонений тренда от фактических значений. Именно для этого количества гармоник и определяют параметры уравнения колеблемости.

Точность модели прогноза может быть оценена с помощью показателя относительной ошибки аппроксимации:

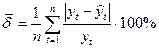
Данный показатель используется для сравнения точности прогнозов по различным моделям. Точность прогноза принято считать высокой при значении показателя меньше 10%, если его значения от 10% до 20%, то точность считается хорошей, 20-50% - удовлетворительной.

На заключительном этапе прогнозирования необходимо определить ошибку полученного прогноза.

Для получения достаточно надежных границ прогноза положения тренда, скажем, с вероятностью 0,95 того, что ошибка будет не больше указанной, следует среднюю ошибку умножить на величину критерия Стьюдента при указанной вероятности (или значимости 1-0,95 = 0,05) и при числе степеней свободы, равном n-2. Предельная ошибка с заданной вероятность определяется как:

где: - средняя ошибка прогноза.

В этом случае, с вероятностью 0,95 можно ожидать, что тренд для момента времени t_k пройдет между значениями и .

Стандартная ошибка прогноза определяется по формуле:

где:

- оценка остаточной дисперсии;

v - период упреждения.

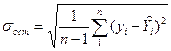
Средняя ошибка прогноза:

Дата добавления: 2014-10-22