Методы выявления тенденций

При выявлении типа тенденции прежде всего необходимо установить:

Ø были ли условия развития объекта достаточно однородными в изучаемый период;

Ø какой характер действия основных факторов развития;

Ø не произошло ли существенное качественное изменение условий развития объекта внутри изучаемого периода времени.

Например, при техническом перевооружении предприятия, скорее всего общая тенденция его развития не сохранится. Поэтому в подобных случаях прибегают к «периодизации» ряда, т.е. его дроблению на отдельные подпериоды: до реконструк­ции, во время таковой (если она длительна) и после освоения новой технологии. Чем крупнее изучаемая система, чем больше факторов влияют на динамику изучаемого признака, тем реже возможны резкие, скач­кообразные изменения в ряду динамики.

При выборе типа трендовой функции используют анализ цепных характеристик интенсивности динамики ряда, так, как это показано в табл. 8.5.

Таблица 8.5

Соответствие типа выбранной функции цепным характеристикам динамического ряда

Цепные характеристики интенсивности динамики ряда	Рекомендуемый тип трендовой функции
Цепные абсолютные приросты относительно стабильны и не имеют четкой тенденции к росту или уменьшению.	Линейная
Цепные темпы роста относительно стабильны и не имеют четкой тенденции к росту или уменьшению.	Парабола
Цепные темпы приросты относительно стабильны и не имеют четкой тенденции к росту или уменьшению.	Экспоненциальная
Прочие варианты	Иные функции.

В статистическом прогнозировании используются следующие основные типы уравнений тренда:

Линейная форма тренда:

где:

- уровни, освобожденные от колебаний, выровненные по прямой;

а - начальный уровень тренда в момент или период, принятый за начало отсчета времени t;

b - среднегодовой абсолютный прирост (среднее изменение за еди­ницу времени); константа тренда.

Параболическая форма тренда:

где: с - квадратический параметр, равный половине ускорения; константа параболического тренда. Под ускорением понимается разность между абсолютным изменением за данный период и абсолютным изменением за предыдущий период:

Остальные обозначения прежние.

Экспоненциальная форма тренда:

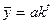
где k - темп изменения в разах; константа тренда.

Логарифмическая форма тренда:

Логарифмическая парабола:

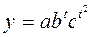
Тренд в форме степенной кривой:

где b - константа тренда.

Гиперболическая форма тренда:

Логистическая форма тренда:

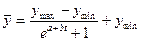
Каждый тип уравнения тренда при анализе и прогнозировании развития экономических явлений выра­жает те или иные качественные свойства развития. Основные рекомендации по применению той или иной функции тренда, в зависимости от особенностей развития тех или иных явлений, приведены в табл. 8.6.

После теоретического исследования особенностей разных форм тренда необходимо обратиться к фактическому ряду динамики, так

Таблица 8.6.

Соответствие типа тренда основным качественным характеристикам развития явления

Тип трендовой функции	Особенности применения трендовой функции в зависимости от качественных характеристик развития явления	Примеры применения
Линейный	Отражает тенденцию изменений при действии множества разнообразных факторов, изменяющихся раз­личным образом по разным закономерностям. Равнодействующая этих факторов при взаимном погашении особенностей отдельных факторов (ускорение, замедление, нелинейность) часто выражается в примерно постоянной абсолютной скорости изменения, т.е. в пря­молинейном тренде.	Тенденции динамики уро­жайности для масштаба области, республики, крупного региона, страны в целом.
Параболический	Выражает ускоренное или замед­ленное изменение уровней ряда с постоянным ускорением. Параболическая форма тренда с отрицательным ускорением (с < 0) приводит со временем не только к приостановке роста уровня, но и к его снижению со все большей скоростью. Такой характер раз­вития может быть свойствен производству устаревшей продукции, ликвидируемой отрасли сельского хозяйства на предприятии (фер­ме) и т.п.	Ускоренный характер развития можно ожидать при наличии важных факторов прогрессивного развития (прогрессирующее поступление нового высокопроизводительного оборудования, увеличение среднесуточ­ного прироста живого веса поросят с возрастом и т.п.). Ускоренное возрастание может также происходить в период после снятия каких-то сдерживающих развитие преград - ограничений в распределении дохода, в уровне оплаты труда, при повышении цены реализации на дефицитную продукцию.

Продолжение табл. 8.6

Экспоненциальный с показателем степени больше 1.	Выражает тенденцию уско­ренного и все более ускоряющегося возрастания уровней. При росте по экспоненте абсолютный прирост пропорционален достигнутому уровню. Рост любого объекта по экспо­ненциальному закону может продолжаться только небольшой исто­рический период времени, ибо ресурсы для любого процесса разви­тия всегда встретят ограничения.	Такой характер свойствен размножению организмов при отсут­ствии ограничения со стороны среды: кормов, пространства, хищ­ников, болезней.
Экспоненциальный с показателем степени меньше 1.	Экспоненциальный тренд означает тенденцию постоянно все более замедляющегося снижения уровней динамического ряда.	Тенденция может быть присуща динамике трудоемкости про­дукции, удельных затрат топлива, металла на единицу полезного эффекта (на 1 кВт ч, на 1 м^2 жилой площади и т.д.) при технологи­ческом прогрессе.
Логарифмический	Пригоден для отображения тенденции замедляющегося роста уровней при отсутствии предельного воз­можного значения.	Пригоден для отображения роста спортивных достижений, роста производительности агрега­та по мере его освоения и совершенствования, повышения продук­тивности скота или вообще эффективности системы при ее совер­шенствовании без качественных, коренных преобразований.
Степенной	Пригоден для отображения измене­ний с разной мерой пропорциональности изменений во времени.	Жестким условием является обязательное прохождение через начало координат.

продолжение табл. 8.6

Гиперболический	Подходит для отображения тенденции, процессов, огра­ниченных предельным значением уровня.	Предельный коэффици­ент полезного действия двигателя, предел 100%-ной грамот­ности населения и т.п.
Логистический	Отражает тенденцию от ускоряющегося роста к равномерному (вогнутость) и от равномерного роста посреди периода к замедляющемуся (вы­пуклость). Подходит для отображения развития в течение дли­тельного периода, проходящего все фазы.	Используется для описания процесса насы­щения потребительского рынка каким-то новым товаром: сначала медленный, но все ускоряющийся рост, затем рост равномерный.

как не всегда можно надежно установить, какой дол­жна быть форма тренда из теоретических соображений. По фактическому динамическому ряду тип тренда устанавливают на основе графического изображения, на основе статистической проверки гипотезы о постоян­стве параметра тренда и другими способами.

После логического анализа динамического ряда и выбора гипотезы о соответствующей форме тренда, необходимо подтвердить реальность (или возможность) использования данной гипотезы. Наиболее обоснованным приемом выявления тренда является про­верка статистической гипотезы о постоянстве того или иного по­казателя динамики. Рассмотрим этот прием по данным табл. 8.7.

В первую очередь проверяется гипотеза о наиболее простой - ли­нейной форме уравнения тренда, т.е. о несущественности разли­чий цепных абсолютных изменений. По данным, приведенным в табл. 8.7. имеем 12 абсолютных изме­нений скользящей средней, которая хотя и сгладила сильные коле­бания уровней ряда, но как видим, ее абсолютные изменения дале­ко не одинаковы. Разбиваем эти 12 цепных приростов на два подпериода: по 6 приростов в каждом, и для каждого подпериода вычисляем среднюю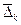, среднее квадратическое отклонение как оценку генерального среднего квадратического отклонения с учетом потери одной степени свободы ва­риации, S

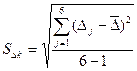
и среднюю ошибку среднего изменения :

Таблица 8.7

Проверка гипотезы о линейном тренде индекса цен (1990 г. = 100%)

Годы	Уровни yi	Средние скользящие за 5 лет,	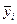Цепные приросты,
		110,0
		113,8	+3,8
		114,2	+0,4
		110,6	-3,6
		107,6	-3,0
		105,8	-1,8
		103,6	-2,2
		101,0	-2,6
		101,4	+0,4
		101,4	0,0
		98,0	-3,4
		95,8	-2,2
		97,0	+1,2

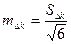
Средняя случайная ошибка разностей двух выборочных средних оценок определяется как корень квадратный из суммы квадратов ошибок каждой из средних, т. е.

Критерий Стьюдента для существенности различия двух средне­годовых приростов (изменений) составит:

Критическое значение критерия при уровне значимости 0,05 и при (6-1) + (6-1) = 10 степенях свободы равно 2,23. Фактическое значение много меньше. Следовательно веро­ятность того, что различие среднегодовых приростов в разные подпериоды случайно, превышает 0,05 и гипотеза о равенстве приро­стов не отклоняется. А значит, тенденцию динамики на всем про­тяжении ряда можно считать линейной.

Дата добавления: 2014-10-22