Уравнение регрессии

Термин регрессия означает, что по известным значениям независимой переменной производят прогноз неизвестных значений зависимой переменной.

Важным этапом регрессионного анализа является определение типа функции, которая характеризует зависимость между факторами. Чаще всего используют следующие типы функций:

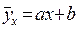– линейную;

– гиперболическую;

– параболическую;

– степенную;

– показательную.

Параметр a называется коэффициентом регрессии, b – свободным членом.

Для нахождения параметров a и b уравнения регрессии используют чаще всего метод наименьших квадратов.

Параметры уравнения прямой a и b можно определить по следующим формулам: , или .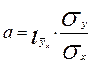

Коэффициент регрессии показывает, на сколько в среднем изменяется величина зависимого (результативного) признака (y) при изменении независимого (факторного) признака (x) на единицу.

Дата добавления: 2014-10-22