Показатели динамики рядов

Общая характеристика рядов динамики

Тема 8. Моделирование и анализ динамики социально-экономических явлений

1. Общая характеристика рядов динамики

2. Показатели динамики рядов

3. Методы выявления тенденций

4. Методика измерения параметров тренда

5. Методика изучения и показатели колеблемости

6. Измерение устойчивости в динамике

7. Сезонные колебания

8. Прогнозирование на основе тренда и колеблемости

9. Смыкание рядов

Ряды динамики – это статистические данные, характеризующие изменения явлений во времени. В зависимости от характера изучаемого явления различают три вида динамических рядов: моментные, интервальные и ряды средних.

Моментными рядами называются ряды статистических величин, показывающие изменения явления на определенную дату (момент времени). Примером могут служить данные счетов бухгалтерского учета, приведенные на 1-ое число каждого месяца. Данные моментных рядов суммированию не подлежат.

Интервальные ряды – это ряды статистических величин, показывающие изменения явления за определенные временные промежутки (периоды времени). Интервальные ряды можно суммировать. Например, производство продукции предприятием за 1 квартал характеризуется следующими данными: январь – 300 тыс. грн., февраль – 305 тыс. грн., март – 306 тыс. грн., всего – 911 тыс. грн.

Ряды, характеризующие изменения средних уровней изучаемого явления во времени, называются рядами средних величин. Например, ряд, приведенный в табл. 8.1.

Таблица 8.1

Среднемесячная заработная плата в Украине, грн.

1995 г.	1996 г.	1997 г.	1998 г.	1999 г.

Ряды средних величин суммировать бессмысленно.

При статистическом изучении динамики необходимо различать понятие тенденции и понятие колеблемости. При изучении динамическое ряда усредненное значение показателей ряда проявляется в динамике как тенденция. В то же время отдельные уровни ряда отклоняются от основной тенденции, испытывая колебания. Для некоторых рядов наблюдаются сезонные колебания - регулярные повторения из года в год.

Тенденция динамики ряда связана с действием долгосрочных причин. Она может измениться, но только в силу изменения степени воздействия этих долгосрочных причин. Колебания отдельных уровней ряда связаны с действием краткосрочных причин. В связи с названными характеристиками тенденции и колеблемости их необходимо четко различать между собой. Смешение тенденции и колеблемости может привести к неверным выводам.

Динамические ряды характеризуются при помощи показателей, определяющих характер, интенсивность, направление. Наиболее простым показателем, характеризующим динамический ряд, является показатель среднего уровня ряда. Он определяется в зависимости от вида динамического ряда. Если ряд моментный с равными промежутками между датами, то используют формулу средней хронологической.

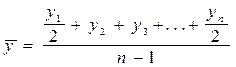, где

y1, y2,...,yn	– фактические значения уровней моментного ряда,
n	– число уровней.

Средний уровень интервального ряда с равными промежутками между датами определяют по средней арифметической простой:

, где

	– средний уровень,
y	– фактические значения уровней ряда,
n	– число уровней.

Если промежутки между датами не равные, то средний уровень ряда вычисляют по средней арифметической взвешенной.

Различают цепные и базисные показатели динамического ряда. Цепные показатели получают, если каждый уровень последующий сравнивают с предыдущим. Базисные показатели получают, если каждый уровень последующий сравнивают с первоначальным уровнем, принятый за базу сравнения.

Показатель, показывающий скорость роста – абсолютный прирост. Он определяется как разность между двумя сравниваемыми уровнями и показывает на сколько один уровень больше (меньше) по сравнению со сравниваемым уровнем.

– цепной, где

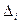
	– абсолютный прирост,
yi	– текущий уровень,
yi-1	– предшествующий уровень ряда.

– базисный, где y₀ – начальный уровень ряда.

Средний абсолютный прирост 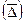рассчитывается по формуле:

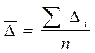, где

	– сумма цепных приростов,
n	– число приростов.

, где

yn	– конечный уровень ряда,
y0	– начальный уровень ряда,
n	– число уровней.

Средний абсолютный прирост показывает на сколько в среднем увеличивается (уменьшается) изучаемое явление.

Коэффициент роста (К_Р) – определяется как отношение двух сравниваемых уровней и показывает, во сколько раз один уровень больше (меньше) по отношению со сравниваемым.

– цепной, – базисный.

Если коэффициенты роста выражают в процентах, то они называются темпами роста (Т_Р):

.

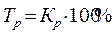Темп прироста показывает на сколько процентов увеличился (уменьшился) текущий уровень по сравнению с базисным, принятым за 100%.Темп прироста можно рассчитать по данным о темпе роста. Для этого надо от темпа роста вычесть 100 или от коэффициента роста – единицу, тогда получим коэффициент прироста.

Т_ПР=Т_Р-100%.

Среднегодовой коэффициент роста определяется по средней геометрической:

, где

K1K2...Kn	– произведение цепных коэффициентов роста,
n	– число коэффициентов роста.

, где

Кбаз	– базисный коэффициент роста за весь период,
n	– число лет.

или 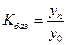, где y_n и y₀ – конечный и первоначальный уровни ряда.

Средний коэффициент роста показывает, во сколько раз в среднем за рассмотренный период изменились уровни динамического ряда.

Средний темп роста определяется по следующей формуле: .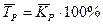

Абсолютное значение одного процента прироста (А%):

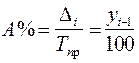, где

Di	– цепной абсолютный прирост,
Тпр	– темп прироста в процентах,
yi-1	– предшествующий уровень ряда.

Данный показатель позволяет правильно оценить темп прироста при сопоставлении его с показателем абсолютного прироста.

Пункты роста – это разность базисных темпов роста (в %):

, где

yi	– текущий уровень ряда,
yi-1	– предшествующий уровень ряда,
у0	– первоначальный уровень ряда, принятый за базу сравнения.

Цепные и базисные характеристики динамики находятся в тесной взаимосвязи. Так, сумма абсолютных приростов равна конечному базисному:

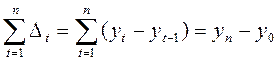
Произведение цепных индексов роста равно конечному базисному:

Рассмотрим расчет вышеуказанных показателей по данным, представленным в табл. 8.2.

Таблица 8.2

Динамика внешнеторгового оборота страны, млн. дол.

Год	Внеш­ний тор­го­вый обо­рот, млн. дол.	Абсолют­ный прирост, млн. дол.	Темп роста, %	Темп прироста, %	Абсо­лютное значе­ние 1% прироста, млн. дол.	Пунк­ты роста, %
		базис­ный	цеп­ной	ба­зис­ный	цеп­ной	ба­зис­ный	цеп­ной
	1040,2	–	–	–	–	–	–	–	–
	1120,3	80,1	80,1	107,7	107,7	7,7	7,7	10,4	7,7
	2654,0	1613,8	1533,7	255,2	236,9	155,2	136,9	11,2	147,5
	2731,8	1691,6	77,8	262,7	103,0	162,7	3,0	26,5	7,5

1886,6 млн. дол.

563,87 млн. дол.

В течение 1994-1997 гг. в среднем внешнеторговый оборот увеличился на 563, 87 млн. дол.

В среднем внешнеторговый оборот увеличивался ежегодно на 37,5% по стране.

Для сравнения тенденции развития нескольких явлений событий, отраженных в соответствующих динамических рядах, применяется способ приведения рядов к одному основанию. Для этого показатели каждого ряда исчисляют в виде базисных темпов роста, как это сделано в табл. 8.3.

Таблица 8.3

Внешняя торговля

Квартал	Экспорт, млн. $	Импорт, млн. $	В процентах к 1 кварталу
			экспорт	импорт
	61,1	35,0	100,0	100,0
	61,0	53,3	99,9	152,3
	57,2	57,1	93,7	163,2
	77,9	39,7	127,5	113,5

По данным табл. 8.3 видна тенденция роста импорта по отрасли.

Для выявления и характеристики основной тенденции ряда используют различные методы сглаживания и аналитического выравнивания динамических рядов.

Суть сглаживания состоит в укрупнении временных интервалов и заменой первичного ряда рядом средних величин. Это позволяет взаимоуравновесить (сгладить) колебания и более четко выразить тенденцию. Для выполнения сглаживания применяют ступенчатые и скользящие средние. Ступенчатые средние получаются путем вычисления средних с определенным шагом, например, первых трех членов ряда, 4-6, 7-9 и т.д. Скользящая средняя вычисляется следующим образом: по формуле средней арифметической находится значение средней для l первых нечетных членов ряда. Каждое последующее значение вычисляетсядля l следующих членов ряда, среди которых убирается первый из предыдущего расчета средней и добавляется следующий. Метод скользящей средней устраняет колебания и четко показывает тренд ряда. В статистической практике могут также использоваться двойные сглаживания на основе скользящей средней, применяются взвешенные скользящие средние.

Однократное аналитическое выравнивание непол­но освобождает параметры тренда от влияния колеблемости, и при сильных колебаниях они могут быть сильно искажены, что в приведенном примере случилось с параболой. Для дальнейшего исключения иска­жающего влияния колебаний на параметры тренда следует приме­нить метод многократного скользящего выравнивания. Этот прием состоит в том, что параметры тренда вычисляются не сразу по всему ряду, а скользящим методом, сначала за первые т периодов времени или моментов, затем за период от 2-го до т + 1, от 3-го до (т + 2)-го уровня и т.п.

Применение методики скользящего многократного выравнивания возможно толь­ко при достаточно большом числе уровней ряда, как правило, 15 и более. Смысл многократного скользящего выравнивания в том, что при последовательных сдви­гах базы расчета параметров на концах ее и в середине окажутся разные уровни с разными по знаку и величине отклонениями от тренда. Поэтому при одних сдвигах базы параметры будут завы­шаться, при других - занижаться, а при последующем усреднении значений параметров по всем сдвигам базы расчета произойдет дальнейшее взаимное погашение искажений параметров тренда коле­баниями уровней.

Многократное скользящее выравнивание не только позволяет полу­чить более точную и надежную оценку параметров тренда, но и осу­ществить контроль правильности выбора типа уравнения тренда. Если окажется, что ведущий параметр тренда, его константа при расчете по скользящим базам не беспорядочно колеблется, а систематически из­меняет свою величину существенным образом, значит, тип тренда был выбран неверно, данный параметр константой не является.

Аналитическое выравнивание состоит в нахождении такой формы функции, ординаты которой были наиболее близки к фактическим значениям ряда. Именно в результате аналитического сглаживания выявляется функция, наиболее близко описывающая тенденцию ряда.

Дата добавления: 2014-10-22