
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейный коэффициент парной корреляции и коэффициент детерминации
|
|
|
|
Наиболее совершенным показателем степени тесноты связи является линейный коэффициент парной корреляции, предназначенный для характеристики прямолинейной связи между x и y. Его значение может изменяться от 0 до ±1. Коэффициент парной корреляции служит показателем интенсивности линейной связи. Он вычисляется по следующей формуле:
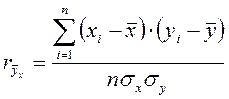 .
.
На практике чаще используется преобразованная формула Пирсона:
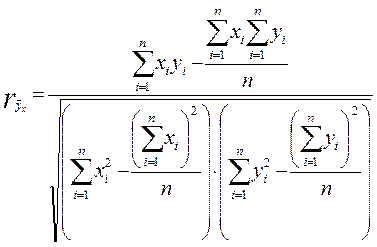 .
.
При использовании этой формулы отпадает необходимость вычислять отклонения индивидуальных значений признаков от средней величины, что позволяет более точно определять коэффициент линейной корреляции, исключив искажения при округлении средних величин и среднего квадратического отклонения.
Ниже приведен расчет коэффициента корреляции по данным показателям оборачиваемости оборотных средств и уровням рентабельности (табл. 7.5):
Таблица 7.5
Расчет коэффициента парной корреляции
| Количество оборотов x | Уровень рентабельности y | xy | x 2 | y 2 |
| 17,0 | 17,0 | 289,0 | ||
| 20,0 | 40,0 | 400,0 | ||
| 25,0 | 75,0 | 625,0 | ||
| 28,0 | 112,0 | 784,0 | ||
| 34,0 | 170,0 | 1156,0 | ||
| Итого: 15 | 124,0 | 414,0 | 3254,0 |
Отсюда

Однако сама величина коэффициента корреляции еще не доказывает достоверность связи между исследуемыми факторами, поэтому его требуется проверить на значимость. Существует множество способов оценки существенности линейного коэффициента корреляции.
Значимость коэффициента корреляции можно проверить при помощи статистики t, которая имеет следующую формулу:
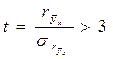 раз,
раз,
где:

| – проверяемый линейный парный коэффициент корреляции, |
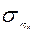
| – стандартная ошибка коэффициента корреляции. |
При малом числе наблюдений  вычисляется по формуле:
вычисляется по формуле:  , а при большом числе наблюдений
, а при большом числе наблюдений  .
.
Применительно к нашему примеру:
 ,
, 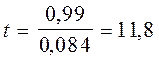 .
.
Следовательно, можно сделать вывод о значимости коэффициента корреляции и связь между факторами не случайна.
Квадрат коэффициента парной корреляции (r 2) называется коэффициентом детерминации. Он показывает, какой удельный вес занимает факторный признак в общей совокупности всех признаков, влияющих на результативный показатель.
Коэффициент линейной корреляции используется при наличии линейной зависимости, при нелинейной зависимости может использоваться такой показатель, как эмпирическое корреляционное отношение (h). Он изменяется от нуля до единицы. Расчет эмпирического корреляционного отношения осуществляется по формуле:
 , где
, где
| s2 | – общая дисперсия, определяемая без поправок на смещение:

|
| d2 | – межгрупповая дисперсия, определяемая:
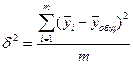 , где , где  – среднее значение каждой i-той группы, – среднее значение каждой i-той группы,
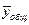 – общая средняя для всех групп,
m – число групп. – общая средняя для всех групп,
m – число групп.
|
Проверка значимости эмпирического корреляционного отношения определяется при помощи статистики t. Стандартная ошибка h определяется как:  , где n – число наблюдений, m – число групп.
, где n – число наблюдений, m – число групп.
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 2316; Нарушение авторских прав?; Мы поможем в написании вашей работы!