Коэффициент корреляции знаков Г.Фехнера

Этот коэффициент был разработан немецким ученым Г. Фехнером. Его расчет основан на сопоставлении знаков отклонений от средней, т.е. вычисляют по средней арифметической простой среднее значение факторного признака (x) и результативного фактора (y). Затем каждое эмпирическое значение факторного и результативного признаков сравнивают со средним 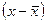и 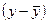, проставляют отклонения в виде знаков.

Коэффициент корреляции знаков определяется по формуле:

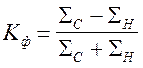, где

SС	– сумма совпадений знаков,
SН	– сумма несовпадений знаков.

Коэффициент корреляции знаков колеблются в пределах от -1 до +1. Чем ближе коэффициент к единице, тем теснее связь. Если все знаки отклонения разные, то коэффициент знаков будет равен -1, что говорит об обратной связи между факторами.

Пример.

Вычислим коэффициент корреляции знаков Фехнера на основании данных о потреблении картофеля в семьях с разным доходом на одного члена семьи в Украине в 1998 г[1]. Соответствующие данные и необходимые расчеты приведены в табл. 7.1.

По данным таблицы имеем: количество совпадений знаков – 7, несовпадений – 1.

Таблица 7.1

Пример расчета коэффициента Фехнера

Доход на одного члена семьи, грн		Количество семей, %	Потребление, кг.
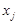
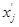
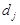
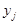
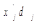
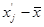
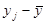
До 30		0,8	69,8	0,1	-100,2	-64,8
30,1-60,0		11,9	111,2	5,4	-70,2	-23,4
60,1-90,0		25,3	129,9	19,0	-40,2	-4,7
90,1-120,0		23,3	146,3	24,5	-10,2	11,7
120,1-150,0		15,0	152,7	20,3	19,8	18,1
150,1-180,0		9,2	152,2	15,2	49,8	17,6
180,1-210,0		5,8	152,7	11,3	79,8	18,1
более 210,0		8,7	161,9	19,6	109,8	27,3
Итого		100,0	1076,7	115,2

Средний доход на одного члена семьи – 115,2 грн.

Среднее потребление картофеля на одного члена семьи – 134,6 кг.

Величина связи:

.

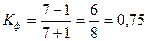Коэффициент Фехнера грубый показатель тес­ноты связи, не учитывающий величину отклонений признаков от средних значений, но он может служить некоторым ориентиром в оценке интенсивности связи. В приведенном примере он указывает на тес­ную связь признаков.

Дата добавления: 2014-10-22