Метод анализа категоризированных переменных и критерий хи-квадрат

В случае альтернативной вариации, т.е. в том случае если вариация исчерпывается только двумя возможностями, выявлении связи некоторого показателя с выделенным фактором рекомендуется использовать метод анализа категоризированных переменных - таблиц сопряженности признаков.

Если обозначить фактор через A, а результативный признак через T, то таблица сопряженности будет выглядеть следующим образом (табл.7.6.):

Таблица 7.6.

Таблица сопряженности

Признак			Итого
А	a	b	a+b
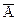
	c	d	c+d
Итого	a+c	b+d	n=a+b+c+d

Признаки считаются независимыми, т.е. между признаками связь является корреляционной, а не функциональной, если соблюдается следующее условие:

;

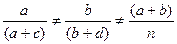Для категоризированных переменных коэффициент связи (или его еще называют коэффициент ассоциации) Q, коэффициент коллигации Y, коэффициент контингенции К_к, дисперсия коэффициента связи 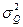, дисперсия коэффициента коллигации 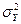, коэффициент Пирсона 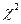(с поправкой на непрерывность) вычисляются по следующим формулам:

;

;

;

;

.

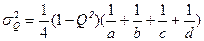В указанной выше формуле определения введена так называемая поправка Йетса. Она применяется, если объем выборки менее 40. При большем объеме выборки определяется по следующей формуле:

;

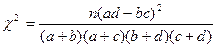Для проверки значимости коэффициента связи и коэффициента коллигации может использовать статистика t. При этом расчетное значение статистики t получают по формулам:

;

Наличие связи считается достаточно доказанным, если t>2.

Достоверность результатов может быть проверена и с помощью критерия Пирсона по указанной выше формуле (с поправкой Йетса или без нее). Фактическое значение сравнивается с табличным для заданного уровня достоверности (значимости) и числа степеней свободы (а в случае рассматриваемой нами четырехпольной таблицы число степеней свободы равно 1).

Пример. Производится исследование влияния пола на отношение к работе. Для этого исследовано 100 работников, из которых 12 мужчин и 88 женщин (табл. 7.7):

Таблица 7.7.

Пример расчета четырехпольной таблицы

Пол	Отношение к работе
	довольны	недовольны	итого
мужской женский
Всего

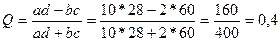
Поскольку наличие связи считается достаточно доказанным, если t>2, то в данном примере связь статистически значимой признать нельзя.

Рассчитаем фактическое значение критерия Пирсона:

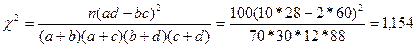
Согласно таблице «Процентные точки распределения c²» для n=1 и Q=5%, .

В нашем примере 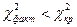. Таким образом наличие связи между признаками не подтвердилось на достаточном уровне значимости, т.е. согласно проведенного исследования статистически значимой связи между полом и отношением к работе обнаружить не удалось.

Дата добавления: 2014-10-22