Коэффициент эластичности

Коэффициент эластичности исчисляется по формуле:

,

где:

a	– коэффициент регресси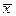и,
и	– средние значения коррелируемых переменных.

Коэффициент эластичности показывает на сколько процентов изменится величина результативного признака (y) при изменении признака-фактора (x) на один процент.

В отличии от коэффициента регрессии коэффициенты эластичности можно сравнивать.

Изучение корреляционной связи одновременно между тремя и более связанными между собой признаками носит название множественной (многофакторной) корреляции. Совокупный коэффициент корреляции характеризует совокупное влияние сразу всех выявленных факторов.

Широкое распространение пакетов прикладных программ позволяет существенно расширить диапазон использования методов корреляционно-регрессивного анализа.

При проведении корреляционно-регрессионного анализа необходимо учитывать «ложную» корреляцию. Она может возникнуть при простом совпадении течения явлений во времени (табл. 7.8).

Таблица 7.8

Пример «ложной» корреляции

Годы	Рост ребенка, x	Высота дерева, y	Nx	Ny
	0,8	2,0
	0,9	3,0
	1,0	4,0

Если вычислить коэффициент корреляции рангов, то он равен r=1. Часто возникает «ложная» корреляция при сопоставлении двух экономических показателей, у которых общий делитель. Примером может служить определение корреляционной связи между показателем технической вооруженности труда и производительностью труда.

Контрольные вопросы к теме 7

1. Какая связь называется функциональной, а какая связь – корреляционной?

2. Какие бывают виды связи по направлению, аналитическому выражению?

3. Как используются диаграммы рассматривания для характеристики выбора связи между явлениями?

4. Какие показатели являются мерой тесноты связи между двумя признаками?

5. Как оценить значимость коэффициентов корреляции?

6. Что характеризует коэффициент детерминации?

7. Какие методы непараметрической статистики вы знаете для изменения связи?

8. Какие показатели используют для измерения тесноты связи между качественными признаками?

9. Что характеризуют параметры уравнения регрессии?

10. Что такое «ложная» корреляция?

Дата добавления: 2014-10-22