Методика измерения параметров тренда

После установления типа тренда вычисляются опти­мальные значения параметров тренда исходя из фактических уров­ней. Для этого обычно используют метод наименьших квадратов (МНК). В данном случае оптимизация состоит в минимизации суммы квадратов отклонений фактических уровней ряда от тренда. Для каждого типа тренда МНК дает систему нормальных уравнений, решая которую вычисляют пара­метры тренда.

Для линейного тренда нормальные уравнения МНК имеют вид:

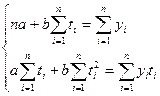
где:

у, - уровни исходного ряда динамики;

_I - номера периодов или моментов времени;

п- число уровней ряда.

Систему можно упростить, перенеся начало отсчета времени t_i в середину ряда. Тогда 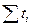(а также суммы всех нечетных степеней t_i) будет равна нулю и система приобретет вид:

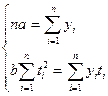
откуда:

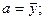
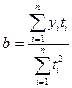
Значения t, расположенные выше средины, имеют отрицательные значения, а расположенные ниже средины – положительные. При нечетном числе членов ряда изменения t даются с интервалом 1, при четном – с интервалом 2, например, -5, -3, -1, 1, 3, 5.

Значения 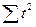определяется по следующим формулам:

для нечетного числа членов ряда:

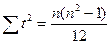
для четного числа членов ряда:

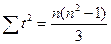
Порядок расчета параметров линейной функции рассмотрим на примере динамического ряда добычи нефти в регионе (табл. 8.8).

Таблица 8.8.

Динамика добычи нефти

Год	yt, млн. т	t	ytt	Yt=74,5+3,8t
	63,5	-3	-190,5	63,1
	66,8	-2	-133,6	66,9
	71,0	-1	-71,0	70,7
	74,3			74,5
	76,9	+1	76,9	78,3
	82,2	+2	164,4	82,1
	86,8	+3	260,4	85,9
Всего	521,5		106,6	521,5

По данным табл. 8.8. имеем:

;

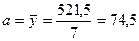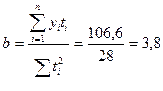
Уравнение линейного тренда выглядит следующим образом:

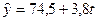
Нормальные уравнения МНК для параболы 2-го порядка имеют вид:

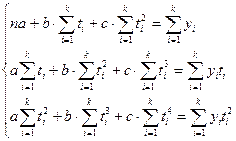
После переноса начала отсчета t в середину ряда имеем:

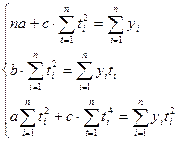
Отсюда:

;

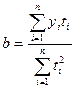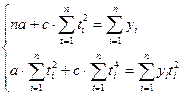
Разделим первое уравнение на n

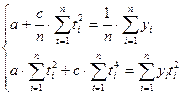
Умножим первое уравнение на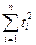

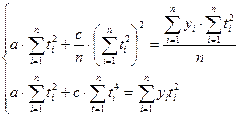
Вычтем из второго уравнения первое:

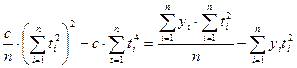
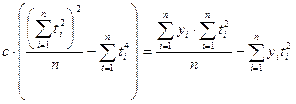
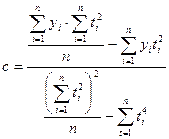
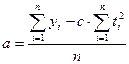
Суммы включают значения t от –(n-1) до +(n-2):2, при этом сумма биквадратов может быть вычислена по формуле:

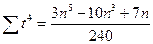
Нормальные уравнения МНК для экспоненты имеют следующий вид:

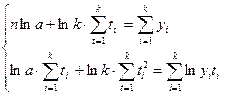
После переноса начала отсчета t, в середину ряда получим:

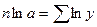, откуда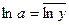

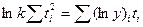, откуда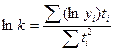

Уравнение логарифмической параболы имеет вид:

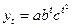
Для определения параметров этого уравнения поместим t=1 в начало ряда и будем его изменять по уровням ряда с шагом равным 1.

Параметры a, b и c уравнения определяются путем потенцирования соответствующих значений, определенных по формулам:

; ;

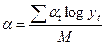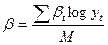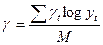
Параметры 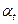, , 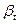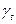и М определяются по специальным таблицам в зависимости от числа уровней исходного динамического ряда [см.Четыркин Е.М. Статистические методы прогнозирования. М.: «Стати­стика». - 1975. - С. 178-179].

Произведем расчет трендового уравнения по данным о производстве электроэнергии в Украине в 2002 г. [исходные данные приводятся на основании: Динаміка виробництва найважливіших видів промислової продукції // Економіст. – 2003. - №9. – С. 48-55]. Результаты расчетов сведены в табл. 8.9.

Таблица 8.9

Расчет параметров трендового уравнения логарифмической параболы по данным о производстве электроэнергии в Украине в 2002 г. (млрд. квт. час.)

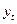
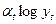
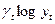
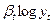
Месяц		t	Табличные значения				Трендовые значения
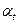
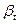
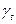
январь				-869		12735,8	-3685,4	233,3
февраль				-451		7963,3	-1879,4	104,2
март				-111		4191,8	-464,8	4,2
апрель					-17	1129,7	624,8	-70,3
май			-273		-29	-1115,5	1368,9	-118,5
июнь			-637		-35	-2584,1	1789,0	-142,0
июль			-819		-35	-3357,5	1922,7	-143,5
август			-819		-29	-3352,0	1714,9	-118,7
сентябрь			-637		-17	-2613,3	1193,8	-69,7
октябрь			-273			-1140,7	355,1	4,2
ноябрь				-199		1145,3	-834,9	104,9
декабрь				-561		4281,1	-2399,3	235,2
Итого	17284,0	-294,6	23,2

Табличное значение М=4004. Следовательно 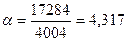; ; 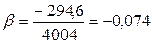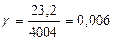. Потенцирование дало следующие результаты: a=20733,867; b=0,844; c=1,013. Искомое уравнение логарифмической параболы имеет вид:

;

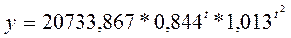Соответствующие трендовые значения, рассчитанные с помощью полученного уравнения приведены в последней колонке табл. 8.9.

5. Методика изучения и показатели колеблемости

Выделяют три основных типа колебаний статистических показателей: пилообразную или маятниковую колеблемость, циклическую долгопериодическую и случайно распределенную во времени колеблемость. Колеблемостью называются отклонения уровней динамического ряда от тренда. свойства и отличия друг от друга хорошо видны при графическом изображе­нии рис. 8.1-8.3.

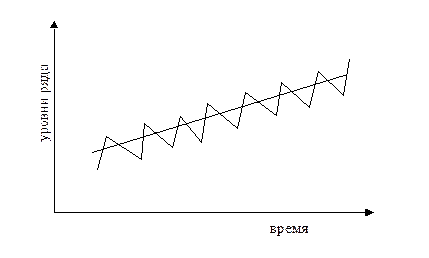Пилообразная или маятниковая колеблемость состоит в попере­менных отклонениях уровней от тренда в одну и в другую сторону (рис. 8.1). Для циклической долгопериодической колеблемости свойственна редкая смена знаков отклонений от тренда и кумулятивный (накапливающийся) эффект отклонений одного знака, который мо­жет тяжело отражаться на экономике (рис. 8.2). Случайно распределенная во времени колеблемость - нерегу­лярная, хаотическая. Она может возникать при наложении множества колебаний с разными по длительности цик­лами либо хаотической колеб­лемости главной причины существования колебаний (рис. 8.3).

Рис. 5.1. Пилообразная или маятниковая колеблемость

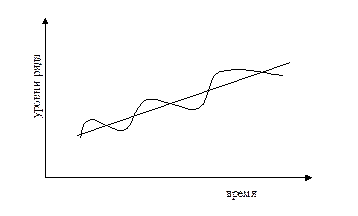
Рис. 5.2. Долгопериодическая циклическая колеблемость

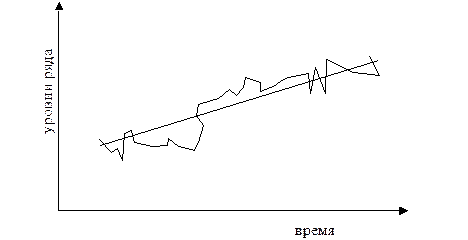
Рис. 5.3. Случайно распределенная во времени колеблемость

Показателями силы колебаний уров­ней являются: амплитуда отклонений уровней отдельных периодов или моментов от тренда (по модулю), среднее абсолютное отклоне­ние уровней от тренда (по модулю), среднее квадратическое откло­нение уровней от тренда. К относительным показателям колеблемости относятся коэффициент колеб­лемости (аналог коэффициента вариации) и от­носительное линейное отклонение от тренда.

Для определения типа колебаний используют следующие методы: графический, метод «поворотных точек» М. Кендалла, вычисление коэф­фициентов автокорреляции отклонений от тренда.

Вариация в пространстве и колеблемость во времени принципиально различны. Эти различия сводятся к следующим:

Ø вызываются разными факторами, из которых одни вызывают влияние на тренд, а другие на колеблемость;

Ø значения варьиру­ющего признака в пространственной совокупности можно считать в основном не зависимыми друг от друга, напротив, уровни дина­мического ряда, как правило, являются зависимыми: это показатели развивающегося процесса, каждая стадия которого связана с пре­дыдущими состояниями;

Ø вариация в пространственной совокупности изме­ряется отклонениями индивидуальных значений признака от сред­него значения, а колеблемость уровней динамического ряда измеря­ется не их отличиями от среднего уровня (эти отличия включают и тренд, и колебания), а отклонениями уровней от тренда.

Для выявления типов колебаний применяют следующие методы:

Ø графический;

Ø поворотных точек Кендалла;

Ø автокорреляции отклонений от тренда.

Графический метод состоит в визуальном распознавании типа колеблемости согласно построенного графика.

Метод поворотных точек Кендалла состоит в подсчете отклонений от тренда и_i. Отклонение, либо большее по алгебраической вели­чине, либо меньшее двух соседних, отмечается точкой. При маятниковой колеблемости все отклонения, кроме двух крайних, будут «поворотными», следовательно, их число со­ставит n-2. При долгопериодических циклах на цикл приходятся один минимум и один максимум, а общее число точек составит 2(п:l), где l - длительность цикла. При случайно распределенной во времени колеблемости число поворот­ных точек в среднем составит: 2/3 (п- 2).

Автокорреляция - это корреляция между уровнями ряда или откло­нениями от тренда, взятыми со сдвигом во времени: на 1 период (год), на 2, на 3 и т.д., поэтому говорят о коэффициентах автокорреляции разных порядков: первого, второго и т. д.

Одна из основных формул для расчета коэффициента автокорре­ляции отклонений от тренда имеет вид:

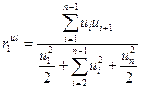
В данной формуле u – отклонения от тренда, т.е.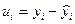

При маятниковой колеблемости все произведения в числителе будут отрицательными величинами, и ко­эффициент автокорреляции первого порядка будет близок к -1. При долгопериодических циклах будут преобладать положительные про­изведения соседних отклонений, а смена знака происходит лишь дважды за цикл. Чем длиннее цикл, тем больше перевес положитель­ных произведений в числителе, и коэффициент автокорреляции пер­вого порядка ближе к +1. При случайно распределенной во времени колеблемости знаки отклонений чередуются хаотически, а число поло­жительных произведений близко к числу отрицательных, ввиду чего коэффициент автокорреляции близок к нулю.

6. Измерение устойчивости в динамике

По отношению к статистическому изучению динамики рассматривается два аспекта понятия «устойчивость»: устойчивость как катего­рия, противоположная колеблемости; устойчивость нап­равленности изменений, т.е. устойчивость тенденции.

В первом понимании показатель устойчивости, который может быть только относительным, должен изменяться от нуля до единицы (100%). Это разность между единицей и относительным показате­лем колеблемости. Если коэффициент колеблемости составил 9,0%, то коэффициент устойчивости равен 100% - 9,0% = 91,0%. Этот показатель характеризует близость фактических уровней к тренду и не зависит от характера последнего. Слабая колеблемость и высокая устойчивость уровней в данном смысле могут существовать даже при полном застое в развитии, когда тренд выражен горизонтальной прямой.

Устойчивость во втором смысле характеризует процесс направленного изменения уровней. С этой точки зрения пол­ной устойчивостью направленного изменения уровней динамического ряда следует считать такое изменение, в процессе которого каждый следующий уровень либо выше всех предшествующих (устойчивый рост), либо ниже всех предшествующих (устойчивое снижение). Вся­кое нарушение строго ранжированной последовательности уровней свидетельствует о неполной устойчивости изменений.

Из определения понятия устойчивости тенденции вытекает и метод построения ее показателя. В качестве показателя устойчивости можно использовать коэффициент корреляции рангов Ч. Спирмэна:

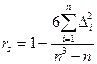
n - число уровней;

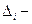разность рангов уровней и номеров периодов времени.

При полном совпадении рангов уровней, начиная с наименьшего, и номеров периодов (моментов) времени по их хронологическому порядку коэффициент корреляции рангов равен +1. Это значение соответствует случаю полной устойчивости возрастания уровней. При полной противоположности рангов уровней рангам лет коэффициент Спирмэна равен -1, что означает полную устойчивость процесса сокращения уровней. При хаотическом чередовании рангов уровней коэффициент близок к нулю, это означает неустойчивость какой-либо тенденции. Приведем расчет коэффициента корреляции Спирмэна по данным о динамике индекса цен (табл. 8.7) в табл. 8.10.

Таблица 8.10

Расчет коэффициентов корреляции рангов Спирмена

Годы	Уровни, yi	Ранг лет, Рx	Ранг уров-ней, Ру	Px-Py	(Px-Py)^2
			9,5	5,5	30,26
			14,5	7,5	56,26
			3,5	4,5	20,26
			1,5	7,5	56,26
			14,5	3,5	12,26
			1,5	12,5	156,26
			3,5	11,5	132,26
			9,5	7,5	56,26
		-	-	-

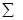
Ввиду наличия трех пар «связанных рангов» применяем форму­лу:

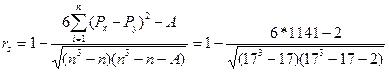
Отрицательное значение коэффициента корреляции рангов Cпирмена указывает на наличие тенденции сни­жения уровней, причем устойчивость этой тенденции ниже средней. При этом следует иметь в виду, что даже при 100%-ной устой­чивости тенденции в ряду динамики может быть колеблемость уровней, и коэффициент их устойчивости будет ниже 100%. При слабой колеблемости, но еще более слабой тенденции, напротив, возможен высокий коэффициент устойчивости уровней, но близкий к нулю коэффициент устойчивости тренда. В целом же оба показа­теля связаны, конечно, прямой зависимостью: чаще всего большая устойчивость уровней наблюдается одновременно с большей устой­чивостью тренда.

Дата добавления: 2014-10-22