Индексный метод анализа динамики среднего уровня

В статистике приходится иметь дело с показателями, которые связаны между собой. Эту связь можно выразить через индексный метод. Система взаимосвязанных индексов позволяет изучать влияние отдельных факторов на изменение сложного явления.

Так, индекс товарооборота зависит от изменения цены и от изменения физического объема товарооборота. Эту связь можно выразить через индексный метод – .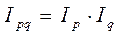

Индекс издержек производства равен произведению индекса себестоимости на индекс физического объема – 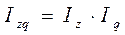. Индекс затрат труда равен произведению индекса трудоемкости на индекс физического объема продукции, т.е. . Необходимость в применении индексов переменного и постоянного состава возникает в том случае, когда динамические уровни общественных явлений выражаются средними величинами.

Индекс постоянного состава определяется по обычной агрегатной форме индекса. Общая формула для всех индексов следующая: . Индекс постоянного состава показывает влияние только одного фактора – самой индексируемой величины.

Индекс переменного состава определяется как отношение двух средних арифметических взвешенных с переменными весами. Его изменение зависит от влияния двух факторов: от изменения самой индексируемой величины и от влияния структурных сдвигов.

Формула индекса переменного состава в общем виде:

.

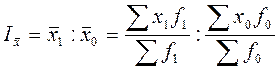Чистое влияние структурных сдвигов определяют отношением индекса переменного состава к индексу постоянного состава, т.е. 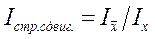. Рассмотрим расчет показателей на следующем примере (табл. 9.4)

Таблица 9.4

Динамика таможенного тарифа на экспортируемую продукцию фирмой «Конус»

	Вид продукции	1 квартал	2 квартал
	Тарифная ставка, %	Сумма экспорта, дол.	Тарифная ставка, %	Сумма экспорта, дол.
А Б В	0,90 0,07 22,00	8240,0 11,2 51296,1	0,96 0,10 24,50	8927,0 14,3 7456,3

Требуется определить:

1. индекс среднего тарифа постоянного состава;

2. индекс среднего тарифа переменного состава;

3. индекс структурных сдвигов.

Вычислим индекс постоянного состава

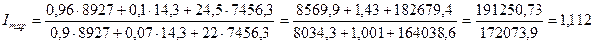
или 111,2%.

Увеличение в среднем таможенного тарифа на 11,2% (111,2%–100%) зависит от изменения тарифной ставки во 2 квартале по сравнению с 1 кварталом.

Определим изменения среднего таможенного тарифа за 1 и 2 кварталы:

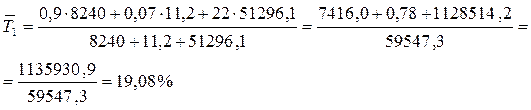
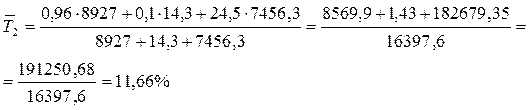
Вычислим индекс среднего таможенного тарифа переменного состава:

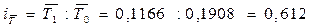или 61,2%

Следовательно, за счет влияния тарифной ставки и сдвигов в структуре экспорта средний таможенный тариф снизился на 38,8% (100%–61,2%). Индекс структурных сдвигов составил:

или 55,1%.

Изменение структуры во 2 квартале повлекло снижение таможенного тарифа дополнительно на 44,9% (100%–55,1%).

Пример 2.

Имеются следующие данные о численности работников в бригадах и их должностном окладе:

	Базисный период	Отчетный период
Ч0	З0	Ч1	З1
№1
№2

Дата добавления: 2014-10-22