Коэффициент корреляции рангов М. Кендалла

Где

n	– число наблюдений,
r^2	– квадрат коэффициента корреляции рангов (коэффициент детерминации).

Статистика t при этом имеет вид: 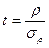, где r – проверяемый коэффициент рангов. При этом t должно оказаться более 3, чтобы с достаточной уверенностью можно было бы сказать, что связь не случайна.

По приведенному примеру:

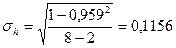
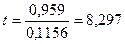
Таким образом, рассчитанная связь не является случайной.

М. Кендалл предложил в качестве меры связи между переменными x и y использовать коэффициент, получивший название «коэффициент корреляции рангов Кендалла». Он вычисляется по формуле:

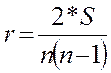
Для расчета S ряды х и y ранжируются в порядке возрастания. Затем по ряду y считается число последующих рангов, превышающих данный (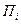) и число последующих рангов, ниже данного (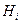). Затем определяется S как:

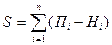
Для примера рассчитаем коэффициент корреляции рангов Кендалла по следующим данным (табл. 7.3):

Таблица 7.3

Расчета коэффициента корреляции Кендалла

Ранги по х	Ранги по Y		s
		15-0
		13-1
		11-2
		11-1
		9-2
		7-3
		6-3
		6-2
		7-0
		3-3
		3-2
		3-1
		3-0
		2-0
		0-1	-1
	Сумма

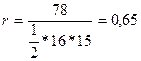
Коэффициент корреляции рангов Кендалла изменяется в пределах от –1 до +1. При достаточно большом числе наблюдений между коэффициентами корреляции рангов Спирмена и Кендалла существует следующее соотношение:

.

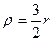Существенность коэффициента корреляции рангов Кендалла проверяется по формуле:

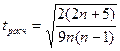
Если в ряду имеются такие значения, для которых невозможно установить разные ранги, то для них вычисляется средний ранг, который приписывается каждому значению. Такой средний ранг может быть и числом дробным. Формула вычисления коэффициента в этом случае выглядит следующим образом:

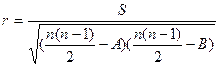, где:

,

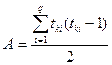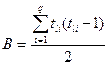
Дата добавления: 2014-10-22