Взаимное положение двух плоскостей

Алгоритм построения прямой, параллельной плоскости

Словесная форма	Графическая форма
1. Через точку D1 провести прямую c1, параллельно a1 (либо b1): c1IIa1, D1Ì c1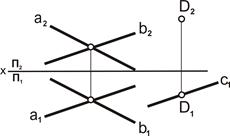
2. Через точку D2 провести c2, параллельно a2. Получаем [m2]II[A2C2], [D2]Ì [m2] Вывод: так как, [m1] II(A1C1], [m2] II [A2C2], то D Ì m, mIIACÞmIIα (ΔABC)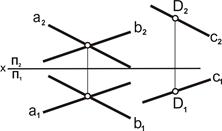

Две плоскости в пространстве могут быть либо взаимно параллельными, в частном случае, совпадая друг с другом, либо пересекающимися. Взаимно-перпендикулярные плоскости представляют собой частный случай пересекающихся плоскостей.

Пересечение двух плоскостей. Линией пересечения двух плоскостей является прямая линия. Проекции прямой линии пересечения двух плоскостей положения определяются проекциями двух точек, принадлежащих одновременно обеим плоскостям. Существует два типа задач на определение линии пересечения плоскостей: построение линии пересечения плоскостей общего положения и построение линии пересечения плоскостей общего и частного положения. Для построения линии пересечения двух плоскостей общего положения используют метод вспомогательных секущих плоскостей-посредников, при этом задачу можно решать двумя способами.

Задача 5.4. Построить линию пересечения двух плоскостей общего положения Ω(ΔDEF) и Σ(ΔABC) (табл. 5.3).

Таблица 5.3

Дата добавления: 2014-10-23