Мета: набути навички дослідження наявності мультиколінеарності засобами MS EXCEL

Тема: дослідження наявності мультиколінеарності за алгоритмом Фаррара–Глобера

Лабораторна робота 4

Завдання для самостійної роботи

Побудувати економетричну модель на основі даних, наведених у табл. 3.4. Провести дослідження побудованої моделі (за п. 3.6 конспекту лекцій). Здійснити точковий та інтервальній прогнози. (N – номер варіанту).

Таблиця 3.4

Вихідні дані

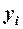
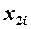
Номер спостереження,	Обсяг виробленої продукції, млн.. грн.,	Обсяг інвестицій, млн.. грн.	Рівень інфляції, %,	Розмір ОВФ, млн. грн.,
	155,0+N/10	42,2	10,1	620,4
	156,2	44,5	10,0	624,8
	157,3	44,6+N/10	9,9	629,2
	158,7	45,8	9,7	634,8+N/10
	159,8	46,8	9,7	639,2
	160,2+N/10	47,9	9,7	640,8
	161,3	50,9	9,8	645,2
	162,9	50,4	9,6	651,6
	163,0	51,2	9,7	652,7
	163,5	55,7	9,5+N/10	654,5
	163,8	54,2	9,0	655,2
	164,9	53,8+N/10	8,3	659,6
	166,7+N/10	56,2	8,5	666,8
	167,8	56,2	8,2	671,2
	168,9	56,9	8,1+N/10	675,6
	170,1	57,8	7,6	680,4+N/10
	171,8	60,2	7,5	687,2
	172,9+N/10	63,8	6,2	691,6
	173,3	69,7	6,1+N/10	693,2
	175,9	70,2	5,4	703,6+N/10
Прогнозні значення	72,5	5,2	707,5

Завдання. Провести дослідження масиву значень незалежних змінних (таблиця 4.1) на наявність мультиколінеарності за алгоритмом Фаррара–Глобера (за п. 4.3 конспекту лекцій).

Таблиця 4.1

Вихідні дані

№ п/п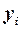
	25,74	4,69	11,97	29,23
	25,34	5,64	13,43	29,35
	31,26	6,26	12,92	33,40
	33,50	6,99	14,74	30,97
	32,30	6,36	14,64	32,92
	38,90	7,60	17,10	37,27
	41,58	7,12	15,63	30,97
	48,02	6,81	15,35	33,58
	43,30	8,67	15,85	35,62
	51,78	7,83	18,05	34,99
	52,14	7,84	17,24	39,34
	54,94	8,85	20,52	41,50
	59,18	9,61	19,18	45,58
	62,22	10,67	19,03	41,08
	63,62	11,04	21,45	40,54
	65,01	11,85	22,25	42,75
	67,78	12,94	24,75	43,89
	71,45	14,24	25,03	41,95
	75,24	15,67	27,87	44,06
	77,38	16,33	30,48	46,77

Виконання завдання:

Завантажуємо програму MS EXCEL. За допомогою буферу обміну переносимо дані таблиці 4.1 на аркуш MS EXCEL.

У рядку 22 обчислюємо середні значення факторних змінних за формулою «=СРЗНАЧ()», у рядку 23 обчислюємо середні квадратичні відхилення факторних змінних за формулою «=СТАНДОТКЛОНП()».

У комірках F2:H21 розраховуємо елементи матриці нормалізованих змінних 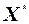за формулою 4.1 з конспекту лекцій:

.

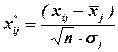Для цього в комірці F2 вводимо команду «=(B2–B$22)/(КОРЕНЬ(20)*B$23)», решту значень нормалізованих змінних знаходимо за допомогою АВТОЗАПОВНЕННЯ (рис. 4.1).

У комірках J2:R4 обчислюємо елементи кореляційної матриці за формулою 4.2. конспекту лекції. Для цього в комірці J2 вводимо команду «=МУМНОЖ(ТРАНСП(F2:H21);F2:H21)», далі діємо за правилами роботи з матрицями.

У комірці К6 обчислюємо за допомогою команди «=МОПРЕД(J2:L4)» визначник матриці .

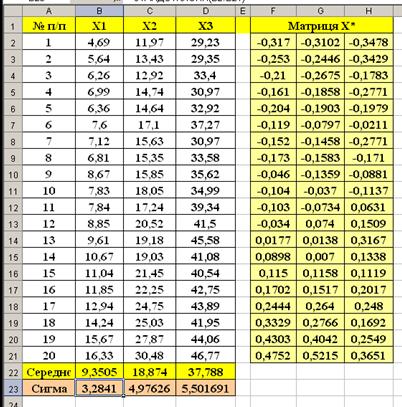
Рисунок 4.1 – Дані до розрахунків

У комірці К8 обчислюємо за формулою 4.3 конспекту лекцій експериментальне значення критерію 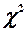. Це значення обчислюється за допомогою команди «=–(20–1–(2*3+5)/6)*LN(K6)».

У комірці К9 знаходимо табличне значення критерію 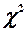при рівні значущості та числі ступенів свободи, рівному 3. Це можна зробити двома способами:

– за допомогою команди «=ХИ2ОБР(0,05;3)»;

– за допомогою Майстра формул, вибравши у розділі «статистические» функцію «ХИ2ОБР» та вказавши потрібні рівень значущості (ймовірність) та число ступенів свободи.

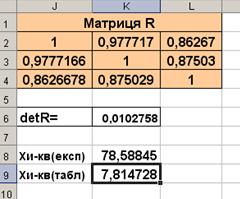
Рисунок 4.2 – Результати розрахунків

У комірках J12:L14 розраховуємо елементи матриці помилок за допомогою команди «=МОБР(J2:L4)».

У комірках К17:К19 обчислюємо експериментальні значення 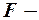критеріїв (формула 4.5 конспекту лекцій). Для цього у комірці К17 набираємо команду «=(J12–1)*(20–3)/(3–1)», у комірці К18 – команду «=(K13–1)*(20–3)/(3–1)», у комірці К19 – команду «=(L14–1)*(20–3)/(3–1)».

У комірці К20 знаходимо табличне значення 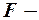критерію. Це можна зробити двома способами:

– за допомогою команди «==FРАСПОБР(0,05;17;2)»;

– за допомогою Майстра формул, вибравши у розділі «статистические» функцію «FРАСПОБР» та вказавши потрібні рівень значущості (ймовірність) та числа ступенів свободи 17 та 2.

У комірках К23:К25 обчислюємо коефіцієнти детермінації для кожної незалежної змінної (формула 4.6 конспекту лекцій). Для цього у комірці К23 виконуємо обчислення за формулою «=1–1/J12», інші два коефіцієнти детермінації знаходимо за допомогою АВТОЗАПОВНЕННЯ.

У комірках N16:N18 обчислюємо часткові коефіцієнти кореляції (формула 4.7 конспекту лекцій). Для цього у комірці N16 набираємо команду «=–K12/КОРЕНЬ(J12*K13)», у комірці N17 – команду «=–L12/КОРЕНЬ(J12*L14)», у комірці N18 – команду

«=–L13/КОРЕНЬ(K13*L14)».

У комірках N20:N22 обчислюємо експериментальні значення критеріїв для кожної незалежної змінної (формула 4.8 конспекту лекцій). Для цього у комірці N20 виконуємо обчислення за формулою «=ABS(N16)*КОРЕНЬ((20–3)/(1–N16^2))», інші два значення знаходимо за допомогою АВТОЗАПОВНЕННЯ.

У комірці N23 знаходимо табличне значення критерію. Це можна зробити двома способами:

– наприклад, за допомогою команди «=СТЬЮДРАСПОБР(0,05;17)»;

– за допомогою Майстра формул, вибравши у розділі «статистические» функцію «СТЬЮДРАСПОБР» та вказавши потрібні рівень значущості (ймовірність) та число ступенів свободи.

Рисунок 4.3 – Результати розрахунків

Висновки:

У ході виконання лабораторної роботи проведено дослідження масиву значень незалежних змінних на наявність мультиколінеарності.

Так як 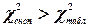, то в масиві незалежних змінних існує мультиколінеарність у сукупності.

Оскільки кожне експериментальне значення критерію більше від табличного: робимо висновок, що кожна незалежна змінна мультиколінеарна з іншими.

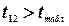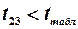Оскільки для експериментальних значень критерію маємо: ,,, то між першою та дру­гою незалежними змінними існує мультиколінеарність.

Висновок: у масиві незалежних змінних існує мультиколінеарність. Доцільно виключити з масиву незалежних змінних або змінну 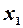або змінну 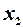та будувати двохфакторну лінійну модель.

Дата добавления: 2014-10-23