Мета: набути навички тестування наявності гетероскедастичності засобами MS EXCEL

Тема: Перевірка гіпотези про відсутність гетероскедастичності при побудові однофакторної економетричної моделі

Лабораторна робота 5

Завдання для самостійної роботи

Провести дослідження масиву значень чотирьох незалежних змінних (таблиця 4.2) на наявність мультиколінеарності за алгоритмом Фаррара–Глобера (N – номер варіанту).

Таблиця 4.2

Вихідні дані

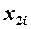
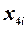
	255,0+N/10	142,2	20,3	320,4
	256,2	144,5	20,2	324,8
	257,3	144,6+N/10	19,9	329,2
	258,7	145,8	19,7	334,8+N/10
	259,8	146,8	19,7	339,2
	260,2+N/10	147,9	19,7	340,8
	261,3	150,9	19,8	345,2
	262,9	150,4	19,6	351,6
	263,0	151,2	19,7	352,7
	263,5	155,7	19,5+N/10	354,5
	263,8	154,2	19,0+N/10	355,2
	264,9	153,8+N/10	18,3	359,6
	266,7+N/10	156,2	18,5	366,8
	267,8	156,2	18,2	371,2
	268,9	156,9	18,1+N/10	375,6
	270,1	157,8	17,6	380,4+N/10
	271,8	160,2	17,5	387,2
	272,9+N/10	163,8	16,2	391,6
	273,3	169,7	16,1+N/10	393,2
	275,9	170,2	15,4	403,6+N/10
	276,2	169,1+N/10	14,1+N/10	405,1
	277,6	172,3	14,5	405,9
	278,2	173,5	13,5	410,1
	278,1+N/10	174,0	12,7	412,2
	280,0	175,0	12,0	415,0

Завдання. Перевірити, застосовуючи параметричний тест Гольдфельда – Квандта, гіпотезу про відсутність гетероскедастич­ності для побудови моделі, яка характеризує залежність заощаджень від доходів населення. Вихідні дані наведені в табл. 5.2.

Таблиця 5.2

Вихідні дані до задачі

Рік	Заощадження	Дохід
	1,36	14,87
	1,20	14,40
	1,70	13,80
	1,84	15,60
	2,10	15,94
	1,12	16,90
	1,89	17,70
	2,30	18,67
	2,50	18,04
	1,17	19,50
	1,90	21,40
	1,95	22,70
	2,87	25,70
	2,60	27,18
	1,75	28,90
	1,96	29,45
	1,40	30,07
	2,99	30,20

Виконання завдання:

Ідентифікуємо змінні: – заощадження (залежна змінна); 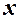– доходи населення (незалежна змінна).

Завантажуємо програму MS EXCEL. За допомогою буферу обміну переносимо дані таблиці 5.2 на аркуш MS EXCEL (у комірках А1:С1 записуємо заголовки, у комірках А2:С19 розташовуємо числові дані таблиці 5.2).

1-й крок

Сортуємо дані за зростанням значення факторної змінної 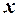. Встановлюємо курсор у тій комірці, де записане перше емпіричне значення факторної змінної 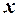(комірка С2). У Головному меню натискаємо «Данные Сортировка». При цьому відкриється вікно «Сортировка диапазона». Встановлюємо параметри «Сортировать по возрастанию » та натискаємо «ОК».

2-й крок

Обчислюємо кількість спостережень, які не будуть ураховані:

.

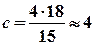Залишається 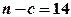спостережень, тобто дві сукупності по 7 спостережень. Отже, для побудови першої моделі будуть використані дані з комірок В2:С8, а для побудови другої моделі будуть використані дані з комірок В13:С19.

3-й крок

За допомогою функції «=ЛИНЕЙН()» знаходимо параметри лінійних моделей. Для побудови першої моделі використаємо дані з комірок В2:С8, а для побудови другої моделі використаємо дані з комірок В13:С19. результати побудови представлені на наступному рисунку.

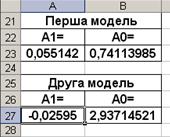
Рисунок 1.1 – Параметри лінійних моделей

Отже, маємо дві лінійні моделі:

4-й крок

У стовпчику D обчислюємо теоретичні значення результативного показника: у комірках С2:С8 – за першою моделлю; у комірках С13:С19 – за другою моделлю.

У відповідних комірках стовпчика Е (комірки Е2:Е8 та Е13:Е19) обчислюємо квадрати відхилень , як квадрати різниць вмісту комірок стовпчиків В та D.

У комірках Е9 та Е20 обчислюємо суми квадратів залишків 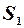і . У комірці Е22 обчислюємо експериментальне значення критерію як відношення до .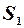

Знаходимо табличне значення 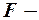критерію. Для цього розташуємо курсор у комірці Е23 і скористаємося можливістю Майстра функцій (функція «=FРАСПОБР()» із категорії «Статистические»).

Результати розрахунків представлені на рис. 5.2.

Рисунок 5.2 – Результати розрахунків

Висновки:

У ході виконання лабораторної роботи, шляхом застосування параметричного тесту Гольдфельда – Квандта, перевірено гіпотезу про відсутність гетероскедастич­ності для побудови моделі, яка характеризує залежність заощаджень від доходів населення. Оскільки 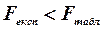, то гетероскедастичність відсутня. Отже, МНК-оцінки параметрів регресійної моделі можуть застосовуватися для подальших досліджень.

Дата добавления: 2014-10-23