Многозвенного механизма

Задача К-3 Определение скоростей и ускорений точек

Ускорение точки тела при плоском движении

Ускорение точки при плоском движении тела равно геометрической сумме ускорения полюса и ускорения точки при вращении вокруг полюса:

,

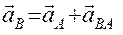где 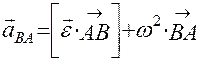- ускорение точки В при вращении вокруг полюса А.

Дано: плоский механизм состоит из 1, 2, 3 и ползунов В и Е (рис. К 3.8, К 3.9) или из стержней 1, 2, 3, 4 и ползунов В или Е (рис. К 3.0 – К 3.7), соединенных друг с другом и с неподвижными опорами О₁, О₂ шарнирами; точки D, В и К находятся в серединах соответствующих стержней. Длины стержней равны соответственно: l₁=0,4 м, l₂=1,2 м, l₃=1,4 м, l₄=0,6 м. Положение механизма определяется углами: α,β,γ,φ,θ. Значения этих углов и других заданных величин указа

ны в таблицах К -3.1 (для рис. К 3.0 – К 3.4) и К 3.2 (для рис. К 3.5 – К 3.9); при этом в табл. К - 3.2 ω₁, ω₄ – величины постоянные.

Определить: скорости и ускорения точек и звеньев плоского механизма, указанные в таблицах в столбцах «Найти».

Указания: построение чертежа следует начинать со стержня, направление которого определяется углом α; дуговые стрелки на рисунках показывают, как при построении чертежа механизма должны откладываться соответствующие углы: по ходу или против хода часовой стрелки.

Заданные угловую скорость и угловое ускорение считать направленными против часовой стрелки, а заданные скорость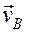и ускорение от точки В к b (рис. К 3.0 – К 3.4).

При решении задачи для определения скоростей точек многозвенного механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и теоремой о распределении скоростей. При определении ускорений точек механизма следует исходить из векторного равенства .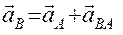

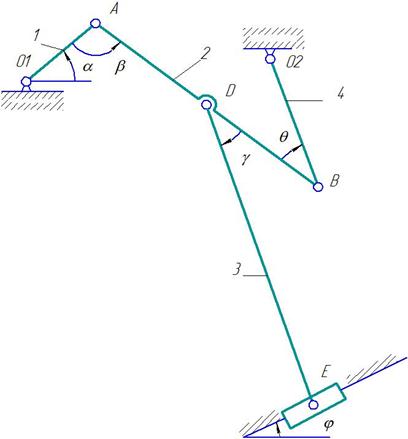
Рис. К 3.0

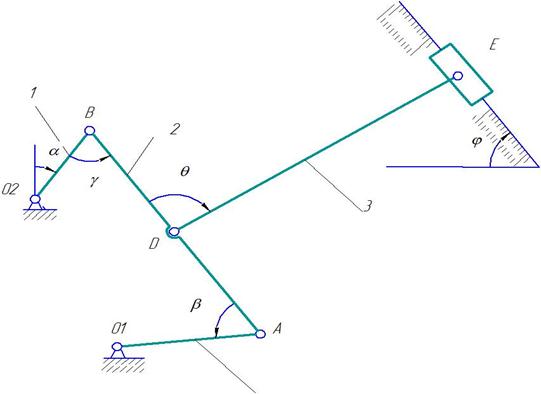
Рис. К 3.1 4

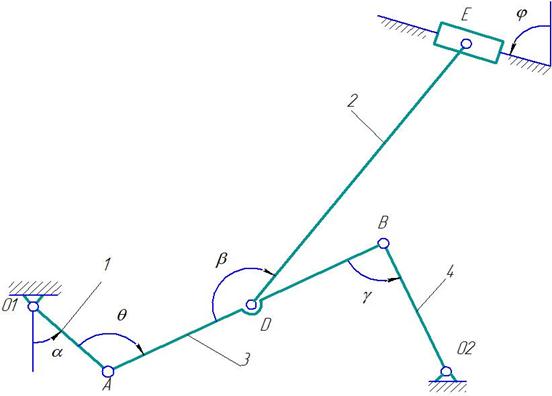
Рис. К3.2

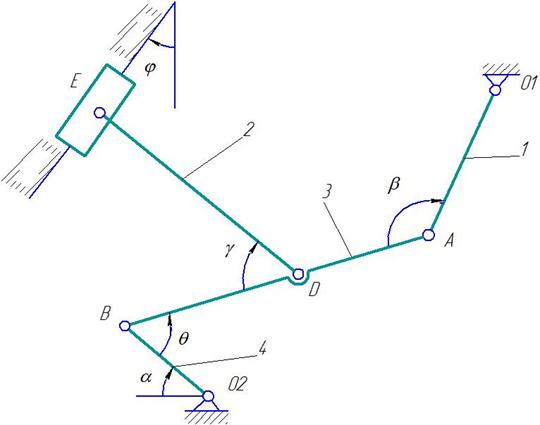
Рис. К.3.3

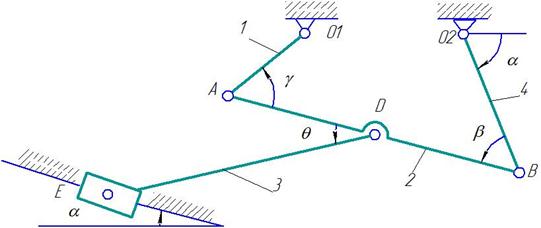
Рис. К 3.4

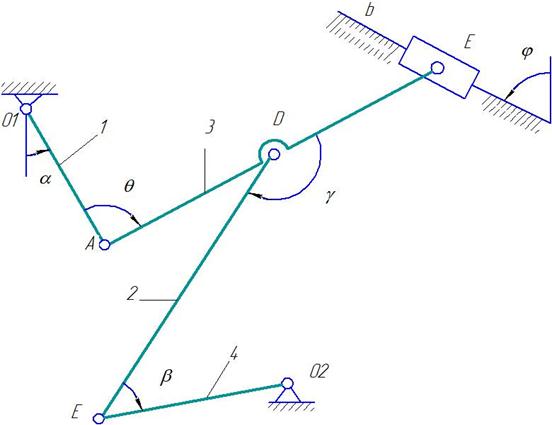
Рис.К 3.5

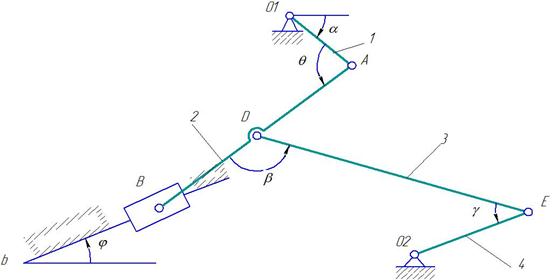
Рис. К 3.6

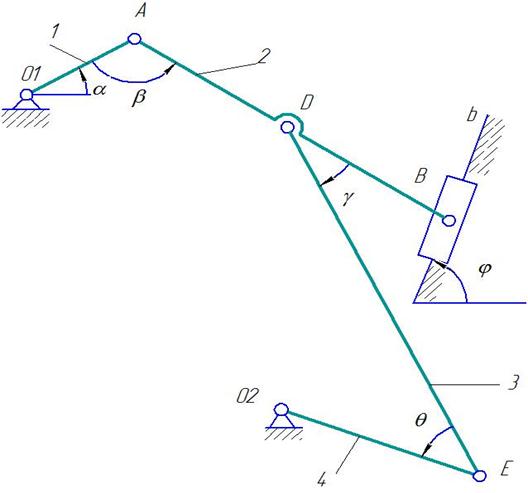
Рис. К 3.7

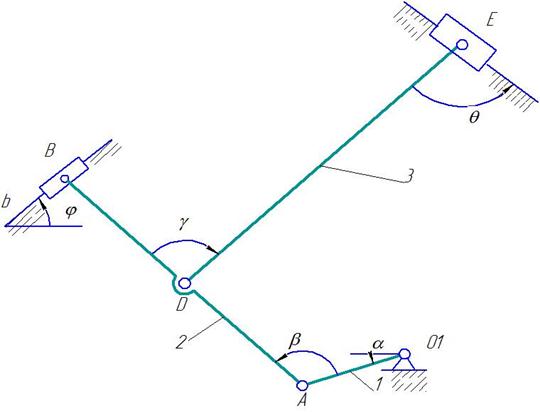
Рис. К 3.8

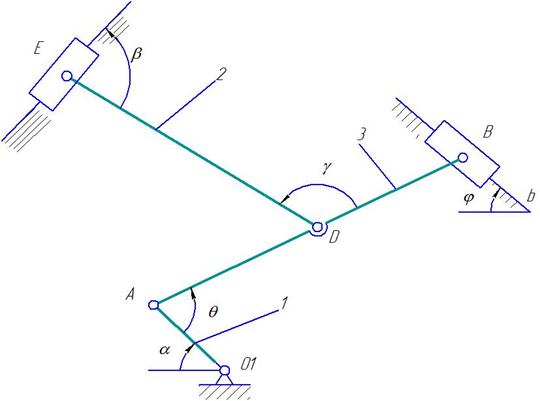
Рис.К 3.9

Таблица К-3.1 (к рис. К 3.0-К 3.4)

Номер условия	Углы, град.	Дано	Найти
α	β	γ	φ	θ	ω1 рад/c	ω4 рад/c	V точек	ω звена	a точки	ε звена
							-	В,Е	DE	В	АВ
						-		А,E	АВ	A	AB
							-	B,Е	AB	B	AB
						-		A,E	DE	A	AB
							-	D,Е	AB	B	AB
						-		A,E	AB	A	AB
							-	B,E	DE	B	АВ
						-		A,Е	DE	A	AB
							-	D,E	AB	B	AB
						-		A,Е	DE	A	AB

Таблица К-3.2 (к рис. К 3.5-К 3.9)

Номер условия

Углы, град.

Дано

Найти

α

β

γ

φ

θ

ω1 рад/c

ε1 рад/c^2

V В м/c

aВ м/c^2

V точек

ω звена

a точки

ε звена

-

-

В,Е

АВ

В

АВ

-

-

А,Е

DE

A

AB

-

-

B,E

АВ

B

AB

-

-

A,E

AB

A

AB

-

-

B,E

DE

B

AB

-

-

D,E

DE

A

AB

-

-

B,E

DE

B

АВ

-

-

A,E

АВ

A

AB

-

-

B,E

DE

B

AB

-

-

D,E

AB

A

AB

Дата добавления: 2014-10-31