Выберите один правильный ответ

ТЕМА 1. События. Алгебра событий. Вероятность случайных событий.

1. Случайные события называются несовместными если осуществление любого из них в результате испытания:

1) исключает осуществление других событий

2) не исключает осуществления других событий

3) обязательно предполагает наступление другого события.

2. Случайные события называются совместными если осуществление любого из них в результате испытания:

1) исключает осуществление других событий

2) не исключает осуществления других событий

3) обязательно предполагает наступление другого события.

3. Совокупность случайных событий А₁, А₂,А₃,…А_n называется полной группой для данного испытания, если в результате испытания:

1) обязательно происходит только одно из событий этой совокупности

2) происходят все события А1, А2,А3,…Аn

3) не происходит ни одно из событий А1, А2,А3,…Аn.

4. Суммой несовместных событий А и В называется такое событие С, в результате которого происходят:

1) либо событие А, либо событие В

2) одновременно события А и В.

5. Произведением совместных событий А и В называется такое событие С, в результате которого происходят:

1) либо событие А, либо событие В

2) одновременно события А и В.

6. При подбрасывании монеты событие А заключается в выпадении герба, В – цифры. Образуют ли события А и В полную группу?

1) да

2) нет.

7. При подбрасывании игрального кубика в зависимости от цифры, выпавшей на грани может произойти 6 событий (А₁… А₆). Образуют ли эти события полную группу?

1) да

2) нет.

8. При одном выстреле по мишени, событие А заключается в попадании, событие В – в промахе. Образуют ли события А и В полную группу?

1) да

2) нет.

9. Сумма вероятностей, образующих полную группу равна:

1) 0

2) 1

3) 0<P<1

4) Р>1.

10. В коробке находятся упаковки анальгина, аспирина и амидопирина. При извлечении одной упаковки может появиться анальгин (событие А), аспирин (В) или амидопирин (С). Образуют ли события А и В полную группу?

1) да

2) нет.

11. В формуле классического определения вероятности 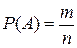, n соответствует:

1) общему количеству испытаний

2) числу всех равновозможных исходов.

12. В формуле статистического определения вероятности 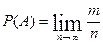n соответствует:

1) общему количеству испытаний

2) числу всех равновозможных исходов.

13. В корзине 4 белых шара, 2 синих и 4 красных. Вероятность извлечения цветного шара равна:

1) 0,4

2) 0,2

3) 0,6

4) 0,8.

14. На столе находятся 15 ампул с новокаином, 25 – с пенициллином и 10 – с лидокаином. Вероятность того, что наугад выбранная ампула окажется ампулой с пенициллином, равна:

1) 0,3

2) 0,5

3) 0,2

4) 0,6.

15. Одновременно подбрасывается 2 монеты. Вероятность того, что хотя бы на одной монете выпадет герб, равна:

1) 0,5

2) 1

3) 0,75

4) 0,25.

16. В коробке находятся 2 новых ампулы и 4 израсходованных. Последовательно извлекаются 2 ампулы. Первая ампула оказалась новой. Вероятность того, что вторая ампула окажется израсходованной, равна:

1) 0,8

2) 0,67

3) 0,33

4) 1.

17. Студент пришел на экзамен, зная 35 из 50 вопросов. На первый вопрос он ответил. Вероятность того, что студент ответит на второй вопрос:

1) 35/50

2) 34/50

3) 35/49

4) 34/49.

18. Брошены две игральные кости. Вероятность того, что сумма очков на выпавших гранях равна семи, составляет:

1) 1/18

2) 1/6

3) 1/12.

19. Брошены две игральные кости. Вероятность того, что произведение очков на выпавших гранях равна 4, составляет:

1) 1/6

2) 1/18

3) 1/12.

20. Одновременно подбрасываются две монеты. Вероятность того, что хотя бы на одной монете выпадет решка:

1) 0,5

2) 1

3) 0,75

4) 0,25.

21. При флюорографическом обследовании 500 студентов, у 100 человек был обнаружен плеврит, у 200 – пневмония. Вероятность заболевания пневмонией равна:

1) 0,2

2) 0,4

3) 0, 5

4) 1.

22. Из 10000 упаковок некоторого препарата, выпущенных фармацевтической фирмой за день, случайным образом отобраны 100 упаковок и среди них обнаружены 3 бракованных. Вероятность того, что упаковка, наугад выбранная из всех выпущенных в этот день, окажется бракованной равна:

1) 0,03

2) 0,003

3) 0,0003.

23. 500 студентов первого курса сдавали экзамен по биологии. Среди 50 наугад выбранных студентов оказались 10 студентов, сдавших экзамен на "отлично". Вероятность сдачи экзамена на «отлично» составляет:

1) 0,01

2) 0,02

3) 0,2

4) 0,5

24. Из 10000 упаковок некоторого препарата, выпущенных фармацевтической фирмой за день, случайным образом отобраны 100 упаковок и среди них обнаружены 3 бракованных. Среднее значение появления бракованных ампул, выпущенных за день, составляет:

1) 3

2) 30

3) 300

4) 3000.

25. 500 студентов первого курса сдавали экзамен по биологии. Среди 50 наугад выбранных студентов оказались 10 студентов, сдавших экзамен на "отлично". Среднее число студентов – отличников составляет:

1) 5

2) 10

3) 100

4) 1000.

Дата добавления: 2014-10-31