Выберите один правильный ответ. ТЕМА 3. Условная вероятность

ТЕМА 3. Условная вероятность. Полная вероятность. Формула Байеса.

Вставьте в логической последовательности значения, слова или фразы

Установите соответствие

13. Между названием теоремы и ее математическим выражением:

1) теорема сложения совместных событий	а) P(AB) = P(A)×P(B)
2) теорема сложения несовместных событий	б) P(A+B) = P(A) + P(B) –P(AB)
3) теорема умножения независимых событий	в) P(A+B) = P(A) + P(B)
4) теорема умножения зависимых событий	г) P(AB)=P(A)×PA(B)

14. Вероятность появления одного из двух _______событий, безразлично какого, равна _______ вероятностей этих событий.

1) совместных

2) несовместных

3) произведению

4) сумме.

15. Вероятность совместного появления двух _________событий равна __________вероятностей этих событий.

1) зависимых

2) независимых

3) совместных

4) сумме

5) произведению.

16. Вероятность совместного появления двух ____событий равна _____вероятности одного из них на _____ вероятность другого, вычисленную в предположении, что первое событие _____.

1) зависимых

2) независимых

3) условную

4) сумме

5) произведению

6) произошло

7) не произошло.

17. Вероятность рождения мальчика – 0,515, вероятность рождения девочки _____, тогда вероятность того, что в семье из двух детей оба мальчика, равна _____.

1) 0,235

2) 0,485

3) 0,5

4) 0,265.

18. Вероятность рождения мальчика – 0,515, вероятность рождения девочки ________, тогда вероятность того, что в семье из двух детей обе девочки, равна ______.

1) 0,235

2) 0,485

3) 0,5

4) 0,265.

19. Вероятность рождения мальчика – 0,515, вероятность рождения девочки ______, тогда вероятность того, что в семье из двух детей дети – разнополые, равна ______.

1) 0,235

2) 0,485

3) 0,5

4) 0,265

1. Понятие «условная вероятность» используется для определения вероятности совместного появления:

1) противоположных событий

2) независимых событий

3) зависимых событий

4) событий, составляющих полную группу.

2. Формула Байеса применяется в случае:

1) определения полной вероятности события А

2) оценки вероятности гипотез до того, как произошло событие А

3) переоценки вероятности гипотез после появления события А

4) определения вероятности совместного появления зависимых событий А и В.

3. Формула Байеса имеет следующую математическую запись

1)

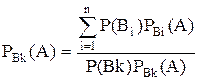
2) Р(А)=Р(В₁)Р_В1(А)+Р(В₂)Р_В2(А)+…+Р(В_n)P_Bn(A);

3)

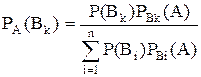
4) Р(А)=Р(А)Р_А(В₁)+Р(А)Р_А(В₂)+…+Р(А)Р_А(В_n).

4. Для переоценки вероятности гипотез после того, как произошло событие А используют формулу:

1)

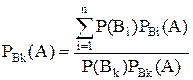
2) Р(А)=Р(В₁)Р_В1(А)+Р(В₂)Р_В2(А)+…+Р(В_n)P_Bn(A);

3)

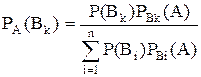
4) Р(А)=Р(А)Р_А(В₁)+Р(А)Р_А(В₂)+…+Р(А)Р_А(В_n).

5. Формула полной вероятности имеет следующую математическую запись:

1) Р(А)=Р(В₁)Р_В1(А)+Р(В₂)Р_В2(А)+…+Р(В_n)P_Bn(A)

2)

3) Р(А)=Р(А)Р_А(В₁)+Р(А)Р_А(В₂)+…+Р(А)Р_А(В_n)

4) .

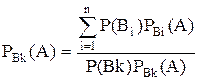6. Для определения полной вероятности события А, которое может наступить при условии появления одного из несовместных событий В₁,В₂,…,В_n, образующих полную группу, используют формулу:

1) Р(А)=Р(В₁)Р_В1(А)+Р(В₂)Р_В2(А)+…+Р(В_n)P_Bn(A)

2)

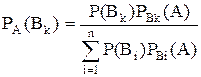
3) Р(А)=Р(А)Р_А(В₁)+Р(А)Р_А(В₂)+…+Р(А)Р_А(В_n)

4) .

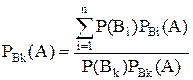7. Произведено испытание, в результате которого произошло событие А, которое может наступить при условии появления одного из несовместных событий В₁,В₂,…,В_n, образующих полную группу. Для того чтобы определить, как изменились вероятности гипотез необходимо найти:

1) условные вероятности гипотез Р_А(В₁), Р_А(В₂),…,Р_А(В_n)

2) условные вероятности Р_В1(А), Р_В2(А),…, Р_Вn(А)

3) полную вероятность события А

4) вероятности гипотез Р(В₁), Р(В₂),…, Р(В_n).

8. В аптечке имеется 5 стандартов анальгина и 3 стандарта нитроглицерина. У вас болит голова. Вероятность достать наугад «нужные» таблетки со второй попытки (не нужная таблетка в аптечку не возвращается):

1) 5/7

2) 3/7

3) 5/8

4) 3/8.

9. В коробке находятся 3 ампулы с порошкообразным лекарством и 3 ампулы с растворителем. Вероятность того, что последовательно будут взяты ампулы сначала с лекарством, потом с растворителем:

1) 1/4

2) 3/10

3) 1/5

4) 1/6.

10. Среди 25 экзаменационных билетов 5 «хороших». Два студента по очереди берут по одному билету. Вероятность того, что оба студента взяли «хорошие» билеты;

1) 4/125

2) 5/120

3) 5/125

4) 1/30.

11. Приема стоматолога дожидаются 4 женщины и двое мужчин. Вероятность того, что врача посетят сначала женщина, а затем мужчина:

1) 16/15

2) 4/15

3) 2/9

4) 3/3.

12. На сельскохозяйственные работы повезли 100 студентов лечебного факультета и 100 – педиатрического. Среди «лечебников» 30 добровольцы. Среди педиатров – 25. Вероятность того, что произвольно выбранный студент окажется добровольцем:

1) 8/40

2) 11/60

3) 11/40

4) 15/60.

13.Студент может пойти в воскресенье на «Столбы» в двух случаях: если будет хорошая погода (р=0,6), если будет свободное время (р=0,4). Вероятность похода при условии хорошей погоды – 0,5, при наличии свободного времени – 0,1. Студент совершит поход на столбы с вероятностью:

1) 0,01

2) 0,55

3) 0,34

4) 0,05.

14.Требуется переливание крови. Среди восьми доноров 5 женщин и трое мужчин. Вероятность того, что «нужная» кровь будет взята у женщины-донора – 0,30, у мужчины – 0,25. Вероятность того, что кровь случайно взятого донора окажется «нужной»:

1) 0,28

2) 0,02

3) 0,58

4) 0,05.

Дата добавления: 2014-10-31