Выберите один правильный ответ. ТЕМА 2. Теоремы сложения и умножения вероятностей

ТЕМА 2. Теоремы сложения и умножения вероятностей.

Несовместных

Вставьте в логической последовательности значения, слова или фразы.

Установите соответствие

Выберите все правильные ответы

26. Выпадение герба или решки при однократном подбрасывании монеты являются событиями:

1) совместными

2) несовместными

3) зависимыми

4) независимыми

5) равновозможными

6) противоположными.

27. Если событие А₁ состоит в выпадении цифры 1 при однократном бросании игрального кубика, а событие А₂ - в выпадении нечётного числа очков, то эти два события:

1) несовместные

2) совместные

3) зависимые

4) независимые

5) равновозможные

6) противоположные.

28. Выпадение цифр 1 или 2 при однократном бросании игрального кубика, являются событиями:

1) зависимыми

2) независимыми

3) совместными

4) несовместными

5) равновозможными

6) противоположными.

29. Если событие А₁ состоит в выпадении цифры 4 при однократном бросании игрального кубика, а события А₂ - чётного числа очков, то эти два события:

1) несовместные

2) совместные

3) зависимые

4) независимые

5) равновозможные

6) противоположные.

30. В ящике находятся белые и чёрные шары, если событие А состоит в том, что при одном извлечении появится белый шар, а событие В - чёрный шар, то эти события:

1) зависимые

2) независимые

3) несовместные

4) совместные

5) равновозможные

6) противоположные.

31. В ящике находятся ампулы с пенициллином и новокаином. Если событие А₁ состоит в том, что при одном извлечении появится ампула с пенициллином, а событие А₂ - ампула с новокаином, то эти события:

1) зависимые

2) независимые

3) несовместные

4) совместные

5) равновозможные

6) противоположные.

32. В ящике находятся 10 белых, 20 синих и 30 красных шаров. Если событие А заключается в том, что при одном извлечении появится синий шар, а событие В – цветной шар, то эти события:

1) зависимые

2) независимые

3) несовместные

4) совместные

5) равновозможные

6) противоположные.

33. Между видом события и его вероятностью:

1) достоверное	а) 0
2) невозможное	б)1
3) случайное	в) 0<p<1
4) противоположное событию А	г) 1- р(А)

34. Классическое определение вероятности справедливо только для ________ и __________ событий.

1) совместных

3) равновозможных

4) зависимых.

1. Вероятность появления одного из двух несовместных событий, безразлично какого, равна:

1) произведению вероятностей этих событий

2) сумме вероятностей этих событий.

2. Сумма вероятностей событий А1, А2, …, Аn, образующих полную группу, равна:

1) 1

2) 0,5

3) 0,3

4) 0.

3. Сумма вероятностей противоположных событий равна:

1) 1

2) 0,5

3) 0,3

4) 0.

4. Вероятность совместного появления двух независимых событий равна:

1) произведению вероятностей этих событий

2) сумме вероятностей этих событий.

5. В урне находится 40 шаров: 10 красных, 10 синих, 15 зеленых, 5 белых. Вероятность того, что при однократном извлечении появится красный или синий шар равна:

1) 0,2

2) 0,5

3) 0,6

4) 1.

6. Предположим, что студент может опоздать на занятия только из-за проблем с транспортом. Вероятность такого опоздания равна 0,3. Тогда вероятность вовремя быть на занятиях равна:

1) 0,2

2) 0,5

3) 0,6

4) 0,7

5) 1.

7. В мешочке находится 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: е, м, и, к, д. Тогда вероятность того, что на вынутых по одному и расположенных «в одну линию» кубиках можно будет прочесть слово «медик» равна:

1)

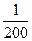
2)

3)

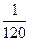
4)

5) .

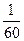8. Вероятность одновременного появления герба на двух монетах при одном подбрасывании равна:

1) 0,5

2) 0,25

3) 1

4) 0.

9. Вероятность события В, вычисленная в предположении, что событие А уже произошло, называется:

1) зависимой

2) независимой

3) полной

4) условной.

10. Студент пришел на экзамен, зная 90 вопросов из 100. В билете три вопроса. Тогда вероятность того, что студент ответит на весь билет равна:

1) 0,9

2) 0,81

3) 0,73

4) 0,5

5) 0,2.

11. В урне 10 шаров: 2 красных, 5 белых; 3 зеленых. Тогда вероятность того, что два раза подряд из урны достанут красный шар (шар в урну возвращают) равна:

1) 0,2

2) 0,4

3) 0,04

4) 0,24.

12. В урне 10 шаров: 2 красных, 5 белых; 3 зеленых. Тогда вероятность того, что два раза подряд из урны достанут красный шар (шар в урну не возвращают) равна:

1)

2)

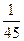
3)

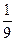
4) .

Дата добавления: 2014-10-31