П. 5. Скалярное, векторное и смешанное произведения векторов

Углом между двумя векторами называется угол, образованный представляющими их отрезками, отложенными от одной точки.

Скалярным произведением двух ненулевых векторов 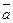и 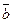называется произведение их длин на косинус угла между векторами, т. е. . Если хотя бы один из векторов 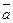, 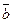нулевой, то .

Свойства скалярного произведения:

, , ,

, ,

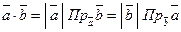в ортонормированном репере .

Направляющими косинусами единичного вектора называются скалярные произведения 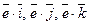, т.е. косинусы углов 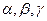, которые вектор образует с осями , причем .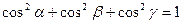

Векторным произведением неколлинеарных векторов 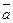и 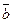называется вектор, обозначаемый и удовлетворяющий условиям

1) ,

2) ,

3) векторы 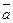, , 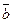образуют правую тройку, т.е. при повороте буравчика от первого перемножаемого вектора к второму вектору по наименьшему углу направление ввинчивания буравчика укажет направление векторного произведения. Если хотя бы один из векторов 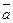, 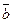нулевой, то =.

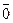Свойства :

, , , ║,

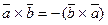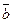Модуль векторного произведения неколлинеарных векторов равен площади параллелограмма, построенного на этих векторах.

Площадь треугольника с вершинами , , : .

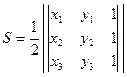Площадь многоугольника с вершинами , ,…, :

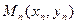Смешанным произведением векторов 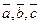называется 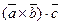. Обозначение .

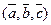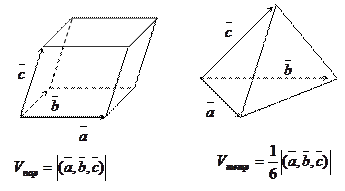Модуль смешанного произведения трех некомпланарных векторов равен объему параллелепипеда, построенного на этих векторах.

Векторы 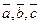компланарны тогда и только тогда, когда их смешанное произведение равно нулю,

т.е. 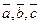компланарны

,

,

,

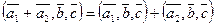Дата добавления: 2014-10-31