
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интегрирование методом подстановки
|
|
|
|
Непосредственное интегрирование
Основные формулы интегрирования
1. 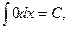 С – константа С – константа
| 1*. 
| |
2. 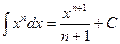 , n ≠ –1 , n ≠ –1
| ||
3. 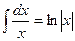 +С +С
| ||
4. 
| 
| |
5.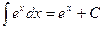
| 
| |
6. 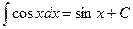
| 
| |
7. 
| 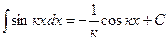
| |
8. 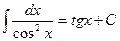
| 
| |
9. 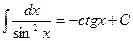
| 
| |
10. 
| 
| 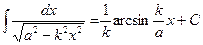
|
11. 
| 
| 
|
| 12. | 
| |
| 13. | 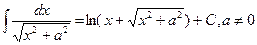
| |
| 14. | 
|
Вычисление интегралов с помощью непосредственного использования таблицы простейших интегралов и основных свойств неопределенных интегралов называется непосредственным интегрированием.
Пример 1. 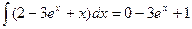
Пример 2. 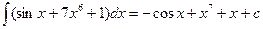
Пример 3. 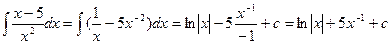
Это наиболее распространенный метод интегрирования сложной функции, состоящий в преобразовании интеграла с помощью перехода к другой переменной интегрирования.
Если интеграл затруднительно привести к табличному с помощью элементарных преобразований, то в этом случае пользуются методом подстановки. Сущность этого метода заключается в том, что путём введения новой переменной удаётся свести данный интеграл к новому интегралу, который сравнительно легко берётся непосредственно.
Для интегрирования методом подстановки используют схему решения:
1) часть подынтегральной функции заменить новой переменной;
2) найти дифференциал от обеих частей замены;
3) всё подынтегральное выражение выразить через новую переменную (после чего должен получиться табличный интеграл);
4) найти полученный табличный интеграл;
5) выполнить обратную замену.
Найдите интегралы:
Пример 1 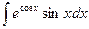 . Подстановка: cosx=t, -sinxdx = dt,
. Подстановка: cosx=t, -sinxdx = dt, 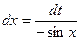
Решение: 
Пример 2. ∫e-x3x2dx Подстановка: -x3=t, -3x2dx=dt, Решение: ∫e-x3x2dx=∫et(-1/3)dt=-1/3et+C=-1/3e-x3+C
Пример 3. 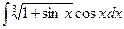 Подстановка: 1+sinx=t, cosxdx=dt,
Подстановка: 1+sinx=t, cosxdx=dt,
Решение: 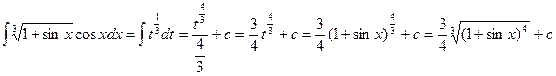 .
.
РАЗДЕЛ 1.5. Определенный интеграл, методы его вычисления.
п.1 Понятие определенного интеграла
Задача. Найти приращение функции, первообразной для функции f(x), при переходе аргумента x от значения a к значению b.
Решение. Положим, что интегрированием найдено: ∫ (x)dx = F(x)+C.
Тогда F(x)+C1, где С1 - любое данное число, будет одной из первообразных функций для данной функции f(x). Найдем её приращение при переходе аргумента от значения a к значению b. Получим:
[F(x)+C1 ]x=b - [F(x)+C1 ]x=a=F(b) +C1 - F(a) -C1 =F(b)-F(a)
Как видим, в выражении приращения первообразной функции F(x)+C1 отсутствует постоянная величина C1. А так как под C1 подразумевалось любое данное число, то полученный результат приводит к следующему заключению: при переходе аргумента x от значения x=a к значению x=b все функции F(x)+C, первообразные для данной функции f(x), имеют одно и то же приращение, равное F(b)-F(a).
Это приращение принято называть определенным интегралом и обозначать символом: 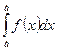 и читается: интеграл от а до b от функции f(x) по dх или, короче, интеграл от а до b от f(х)dх.
и читается: интеграл от а до b от функции f(x) по dх или, короче, интеграл от а до b от f(х)dх.
Число а называется нижним пределом интегрирования, число b - верхним; отрезок а ≤ x ≤ b – отрезком интегрирования. Предполагается при этом, что подынтегральная функция f(x) непрерывна при всех значениях x, удовлетворяющих условиям: a x b
Определение. Приращение первообразных функций F(x)+C при переходе аргумента x от значения x=a к значению x=b, равное разности F(b)-F(a), называется определенным интегралом и обозначается символом: 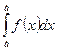 так, что если ∫ (x)dx = F(x)+C, то
так, что если ∫ (x)dx = F(x)+C, то 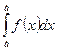 = F(b)-F(a) - данное равенство называется формулой Ньютона - Лейбница.
= F(b)-F(a) - данное равенство называется формулой Ньютона - Лейбница.
п.2 Основные свойства определённого интеграла
Все свойства сформулированы в предложении, что рассматриваемые функции интегрируемы в соответствующих промежутках.
- Определённый интеграл с одинаковыми пределами равен нулю:
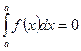
- При перестановке пределов интегрирования знак интеграла меняется на противоположный:
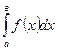 = -
= - 
- Отрезок интегрирования можно разбивать на части:
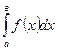 =
= 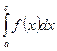 +
+ 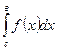 , где а < c < b
, где а < c < b - Постоянный множитель можно выносить за знак интеграла:
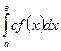 = c
= c 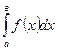 .
. - Интеграл от алгебраической суммы функций равен такой же алгебраической сумме интегралов от всех слагаемых:
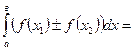
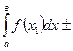
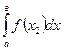
п. 3 Непосредственное вычисление определенного интеграла
Для вычисления определённого интеграла, когда можно найти соответствующий неопределенный интеграл, служит формула Ньютона – Лейбница
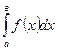 =
= 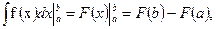
т.е. определённый интеграл равен разности значений любой первообразной функции при верхнем и нижнем пределах интегрирования.
Из этой формулы виден порядок вычисления определенного интеграла:
1) найти неопределенный интеграл от данной функции;
2) в полученную первообразную подставить вместо аргумента сначала верхний, затем нижний предел интеграла;
3) из результата подстановки верхнего предела вычесть результат подстановки нижнего предела.
Пример 1: 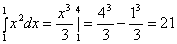 Вычислить интеграл:
Вычислить интеграл: 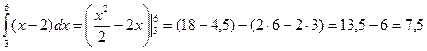
Пример 2: Вычислить интеграл:
п.4 Вычисление определенного интеграла методом подстановки
Вычисление определенного интеграла методом подстановки состоит в следующем:
1) часть подынтегральной функции заменить новой переменной;
2) найти новые пределы определенного интеграла;
3) найти дифференциал от обеих частей замены;
4) всё подынтегральное выражение выразить через новую переменную (после чего должен получиться табличный интеграл); 5) вычислить полученный определенный интеграл.
Пример 1: Вычислить интеграл:
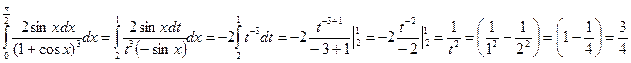
Подстановка: 1+cosx=t, -sinxdx = dt, 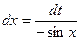
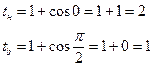
РАЗДЕЛ 1.6. Геометрический смысл определенного интеграла.
Площадь криволинейной трапеции:
Известно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x).
Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.
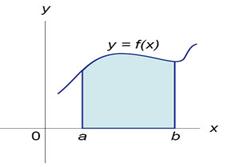 Пусть на отрезке [а; b] задана непрерывная функция у = ƒ(х) ≥ 0. Найдем площадь этой трапеции.
Пусть на отрезке [а; b] задана непрерывная функция у = ƒ(х) ≥ 0. Найдем площадь этой трапеции.
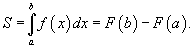 Площадь фигуры, ограниченной осью 0 x, двумя вертикальными прямыми x = a, x = b и графиком функции у = ƒ(х) (рисунок), определяется по формуле:
Площадь фигуры, ограниченной осью 0 x, двумя вертикальными прямыми x = a, x = b и графиком функции у = ƒ(х) (рисунок), определяется по формуле:
В этом заключается геометрический смысл определённого интеграла.
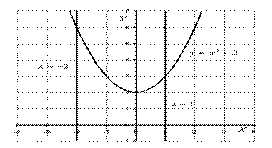 Пример 1: Вычислить площадь фигуры, ограниченной линиями: у=х2.+2, у=0, х= -2, х=1.
Пример 1: Вычислить площадь фигуры, ограниченной линиями: у=х2.+2, у=0, х= -2, х=1.
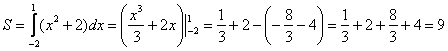 Решение: Выполним чертеж (обратите внимание, что уравнение у=0 задает ось Ох).
Решение: Выполним чертеж (обратите внимание, что уравнение у=0 задает ось Ох).
Ответ: S = 9 ед2
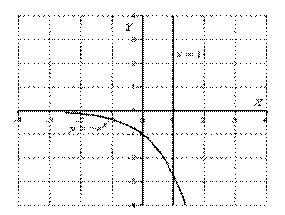 Пример 2: Вычислить площадь фигуры, ограниченной линиями: у= - ех, х=1 и координатными осями.
Пример 2: Вычислить площадь фигуры, ограниченной линиями: у= - ех, х=1 и координатными осями.
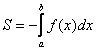 Решение: Выполним чертеж.
Решение: Выполним чертеж.
Если криволинейная трапеция полностью расположена под осью Ох, то её площадь можно найти по формуле:
В данном случае:
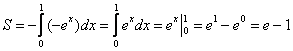
Ответ: 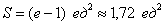
Внимание! Если Вам предложено найти площадь фигуры с помощью определенного интеграла, то площадь всегда положительна! Именно поэтому в только что рассмотренной формуле фигурирует минус.
РАЗДЕЛ 1.7. Применение определенного интеграла
п.1 Вычисление объема тела вращения
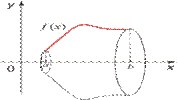 Если криволинейная трапеция прилежит к оси Оx, а прямые у=a, у=b и график функции у= F(x) (Рис.1), тогда объем тела вращения определяется по формуле, содержащей интеграл.
Если криволинейная трапеция прилежит к оси Оx, а прямые у=a, у=b и график функции у= F(x) (Рис.1), тогда объем тела вращения определяется по формуле, содержащей интеграл.
Объем тела вращения равен: 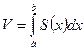
Пример:
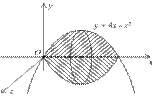 Найти объём тела, ограниченного поверхностью вращения линии
Найти объём тела, ограниченного поверхностью вращения линии 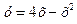 вокруг оси Ох при 0≤ х ≤4.
вокруг оси Ох при 0≤ х ≤4.
Решение: V 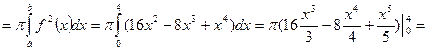
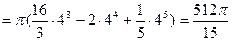 ед3. Ответ:
ед3. Ответ: 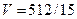
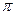 ед3.
ед3.
РАЗДЕЛ 3.1. Обыкновенные дифференциальные уравнения
п.1 Понятие о дифференциальном уравнении
Определение. Дифференциальным уравнением называется уравнение, содержащее функцию от совокупности переменных и их производных.
Общий вид такого уравнения 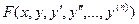 =0, где F- известная функция своих аргументов, заданная в фиксированной области; х - независимая переменная(переменная, по которой дифференцируется);у - зависимая переменная (та, от которой берутся производные и та, которую надо определить);
=0, где F- известная функция своих аргументов, заданная в фиксированной области; х - независимая переменная(переменная, по которой дифференцируется);у - зависимая переменная (та, от которой берутся производные и та, которую надо определить); 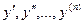 - производная зависимой переменной у по независимой переменной х.
- производная зависимой переменной у по независимой переменной х.
п.2 Основные понятия дифференциального уравнения
Порядком дифференциального уравнения называется порядок старшей производной, входящей в него.
Например:
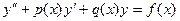 - уравнение второго порядка,
- уравнение второго порядка, 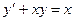 - уравнение первого порядка.
- уравнение первого порядка.
Всякая функция, связывающая переменные и обращающая дифференциальное уравнение в верное равенство, называется решением дифференциального уравнения.
Общим решением дифференциального уравнения первого порядка называется функция 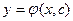 от
от 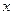 и произвольной постоянной С, обращающая это уравнение в тождество по
и произвольной постоянной С, обращающая это уравнение в тождество по 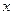 .
.
Общее решение, записанное в неявном виде 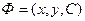 =0, называется общим интегралом.
=0, называется общим интегралом.
Частным решением уравнения 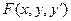 =0 называется решение, полученное из общего решения при фиксированном значении
=0 называется решение, полученное из общего решения при фиксированном значении 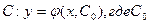 - фиксированное число.
- фиксированное число.
Задача нахождения частного решения дифференциального уравнения n-го порядка (n= 1,2,3,…), удовлетворяющего начальным условиям вида
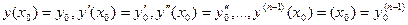 ,
,
называется задачей Коши.
п.3 Дифференциальные уравнения первого порядка с разделяющимися переменными
Дифференциальное уравнение первого порядка 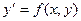 называется уравнением с разделяющимися переменными, если его можно представить в виде
называется уравнением с разделяющимися переменными, если его можно представить в виде 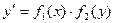 можно переписать в виде
можно переписать в виде 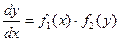 . Если
. Если 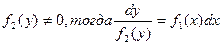 . Интегрируем:
. Интегрируем: 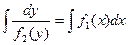 .
.
Чтобы решить уравнение такого вида надо:
1. Разделить переменные;
2. Интегрируя уравнение с разделенными переменными, найти общее решение данного уравнения;
3. Найти частное решение, удовлетворяющее начальным условиям (если они заданы).
Пример 1. Решить уравнение 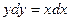 . Найти частное решение, удовлетворяющее условию y=4 при x=-2.
. Найти частное решение, удовлетворяющее условию y=4 при x=-2.
Решение: Это уравнение с разделенными переменными. Интегрируя, находим общее решение уравнения: 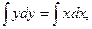
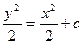 . Для получения более простого по форме общего решения постоянное слагаемое в правой части представим в виде C/2. Имеем
. Для получения более простого по форме общего решения постоянное слагаемое в правой части представим в виде C/2. Имеем 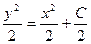 или
или 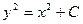 - общее решение. Подставив в общее решение значения y=4 и x=-2, получим 16=4+С, откуда С=12.
- общее решение. Подставив в общее решение значения y=4 и x=-2, получим 16=4+С, откуда С=12.
Итак, частное решение уравнения, удовлетворяющее данному условию, имеет вид 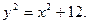
Пример 2. Найдите частное решение уравнения 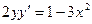 , если
, если 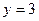 при
при 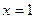 .
.
Решение: 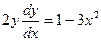 ,
, 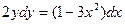 ,
, 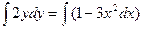 ,
, 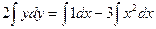 ,
, 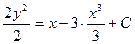 ,
, 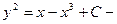 общее решение.
общее решение.
Подставляем значения х и у в частное решение: 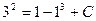 ,
, 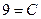 ,
, 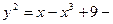 частное решение.
частное решение.
Пример 3. Найдите общее решение уравнения 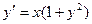 . Решение:
. Решение: 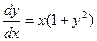 ,
, 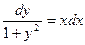 ,
, 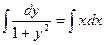 ,
, 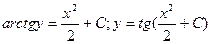 - общее решение.
- общее решение.
п.4 Дифференциальные уравнения порядка выше первого
Уравнение вида 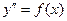 или
или 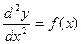 решается двукратным интегрированием:
решается двукратным интегрированием: 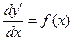 ,
, 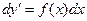 , откуда
, откуда 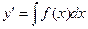 . Проинтегрировав эту функцию, получим новую функцию от f(x), которую обозначим через F(x). Таким образом,
. Проинтегрировав эту функцию, получим новую функцию от f(x), которую обозначим через F(x). Таким образом, 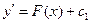 ;
; 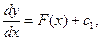
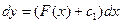 . Интегрируем еще раз:
. Интегрируем еще раз: 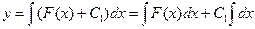 или у=Ф(х)
или у=Ф(х) 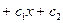 . Получили общее решение уравнения
. Получили общее решение уравнения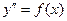 , содержащее две произвольные постоянные
, содержащее две произвольные постоянные 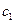 и
и 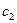 .
.
Пример 1. Решить уравнение 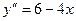 .
.
Решение: 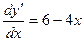 ,
, 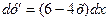 ,
, 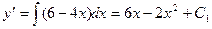 ,
,
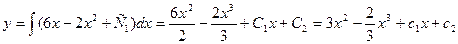
Пример 2. Решить уравнение 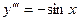 . Решение:
. Решение: 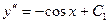 ,
, 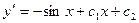 ,
, 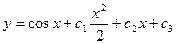 .
.
РАЗДЕЛ 3.2. Числовой ряд, его члены
Определение 1. Числовым рядом называется выражение вида 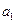 +
+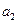 +…+
+…+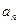 +…, (1)
+…, (1)
где 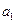 ,
, 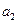 , …,
, …, 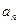 , … — числа, принадлежащие некоторой определенной числовой системе.
, … — числа, принадлежащие некоторой определенной числовой системе.
Так, можно говорить о действительных рядах, для которых 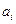
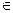 R, о комплексных рядах, для которых
R, о комплексных рядах, для которых 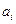
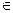 C, i = 1, 2, …, n, …
C, i = 1, 2, …, n, …
Для сокращенного обозначения рядов используется знак суммирования 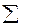 , а именно
, а именно
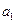 +
+ 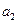 + … +
+ … + 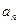 + … =
+ … =  . (2)
. (2)
Определение 2. Числа 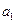 ,
, 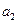 , …,
, …, 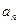 , …называются членами ряда (2); an называется общим членом ряда. Иногда общий член удобнее записывать так, чтобы индекс n принимал значения n = 0, 1, 2,…
, …называются членами ряда (2); an называется общим членом ряда. Иногда общий член удобнее записывать так, чтобы индекс n принимал значения n = 0, 1, 2,…
Определение 3. Ряд (3) называется рядом геометрической прогрессии.
Если, например, a = 1, q = 1/2, то получим ряд 1 + 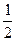 +
+ 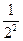 + …+
+ …+ 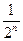 + … =
+ … = 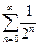 .
.
Определение 4. Ряд 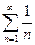 = 1 +
= 1 + 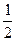 +
+ 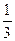 + … +
+ … + 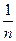 + …, составленный из чисел, обратных натуральным числам, называется гармоническим рядом.
+ …, составленный из чисел, обратных натуральным числам, называется гармоническим рядом.
Другие примеры рядов:
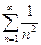 = 1 +
= 1 + 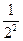 +
+ 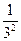 + … +
+ … + 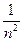 + …,
+ …,
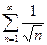 = 1 +
= 1 + 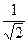 +
+ 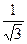 + … +
+ … + 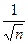 + …
+ …
Определение 5. Сумма первых n членов ряда называется частичной суммой ряда.
Признак Даламбера. Теорема. Пусть дан ряд (1) с положительными членами. Допустим, что 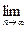
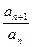 существует и
существует и 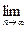
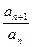 =
= 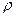 .
.
Тогда:
1) если 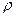 < 1, то ряд (1) сходится;
< 1, то ряд (1) сходится;
2) если 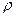 > 1, то ряд (1) расходится;
> 1, то ряд (1) расходится;
3) если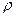 =1, то следует воспользоваться другим признаком сходимости.
=1, то следует воспользоваться другим признаком сходимости.
Пример 1: Исследовать на сходимость ряд: 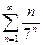 . Решение: Здесь
. Решение: Здесь 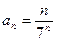 , и поэтому
, и поэтому 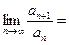
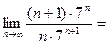
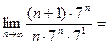
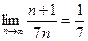 < 1. Следовательно, данный ряд сходится.
< 1. Следовательно, данный ряд сходится.
Пример 2: Исследовать на сходимость ряд 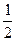 +
+ 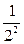 +
+ 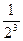 + … +
+ … + 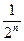 + … =
+ … = 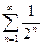 .
.
Решение: 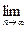
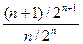 =
= 
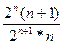 =
= 
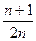 =
= 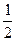 < 1. Следовательно, данный ряд сходится.
< 1. Следовательно, данный ряд сходится.
Пример 3: Исследуйте на сходимость ряд: 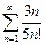 .
.
Решение: Имеем 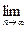
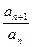 =
= 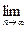
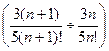 =
= 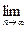
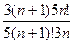 =
= 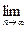
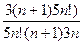 =
=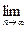
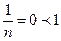 .
.
Раздел 3.3. Основы теории вероятностей и математической статистики
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 9991; Нарушение авторских прав?; Мы поможем в написании вашей работы!