Определение вероятности события

Относительная частота события

Пусть производится некоторое испытание и А – случайное событие, которое может произойти и не произойти в этом испытании.

Если произведено N одинаковых испытаний и М – число испытаний, в котором событие А произошло, то отношение М/N называется частотой наступления события А в данной последовательности испытания.

Частота случайна и зависит от числа N всех испытаний.

Если N достаточно велико, то при его дальнейшем увеличении частота обычно меняется мало, т.е. становится статистически устойчивой.

Случайные события со статистически устойчивой частотой широко распространены в физике, биологии, экономике и других областях знаний.

Статистически устойчивая частота позволяет объективно расценить вероятность наступления события А. Понятие вероятности связано в испытании с опытным понятием статистически устойчивой частоты, а формула m/n≈Р(А) выражает статистический подход к определению вероятности.

Определение: Вероятность события А равна отношению числа m исходов испытаний, благоприятствующих наступлению события А, к общему числу n всех равновозможных несовместных исходов, т.е. Р(А)= 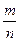. Следовательно, для нахождения вероятности события необходимо, рассмотрев различные исходы испытания, подсчитать всевозможные несовместимые исходы n, выбрать число интересующих нас исходов m и вычислить отношение m к n.

Из этого определения вытекают следующие свойства:

1. Вероятность любого события есть неотрицательное число, на превосходящее единицы.

Действительно, число m искомых событий заключено в пределах 0≤ m≤ n.

Разделив обе части неравенства на n, получим 0 ≤ Р(А) ≤ 1.

1. Вероятность достоверного события равна единице, так как m/n =1
2. Вероятность невозможного события равна нулю, поскольку 0/n=0

Пример: Бросают игральную кость. Найти вероятность того, что:

а) выпадет четное число очков (событие A);

б) выпадет число очков, кратное 3 (событие В);

в) выпадет любое число очков, кроме 5 (событие С)

Решение:

а) На гранях игральной кости имеются три четные цифры (2, 4, 6), т.е. число искомых исходов m=3. Число всех возможных исходов равна 6 (выпадает любое число очков от 1 до 6). Значит, Р(А)=3/6=1/2.

б) Здесь имеются две цифры, кратные трем: 3 и 6. Следовательно, m=2, а число всех возможных исходов n=6, откуда Р(В)=2/6=1/3.

в) Искомыми исходами являются цифры 1, 2, 3, 4, 6 – всего их пять (m=5). Число всех возможных исходов n=6. Поэтому Р(С)=5/6.

При вычислении вероятности часто приходится использовать формулы комбинаторики. Рассмотрим примеры непосредственного вычисления вероятностей.

Пример: В урне 7 красных и 6 синих шаров. Наугад вынимают два шара. Какова вероятность того, что оба вынутых шара красные?

Решение: Число равновозможных независимых событий равно: n= 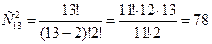. С обытию А благоприятствуют m= 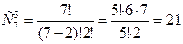. Следовательно,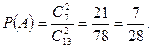

Содержание:

Введение, разделы дисциплины
Требования к выполнению контрольной работы	1-2
Номера вариантов и литература
Задания к контрольной работе	2-4
Краткие вопросы теоретические материала и рекомендации к выполнению заданий	4-15

Дата добавления: 2014-10-31