
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 2.8 Решение задачи линейного программирования
|
|
|
|
с использованием симплекс-таблиц
Приводим систему ограничений задачи ЛП к виду:
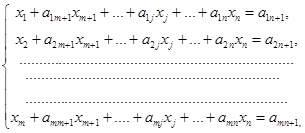
где 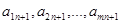 – положительные числа. Целевую функцию записываем в виде:
– положительные числа. Целевую функцию записываем в виде:
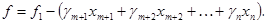
Из коэффициентов системы уравнений и коэффициентов целевой функции составляем первую симплекс-таблицу (таблица 2.2).
Таблица 2.2
| Б.п | 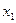
| … | 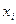
| … | 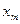
| 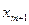
| … | 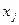
| … | 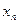
| С.к |
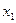
| … | … | 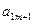
| … | 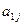
| … | 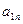
| 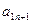
| |||
| … | … | … | … | … | … | … | … | … | … | … | … |
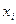
| … | … | 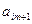
| … | 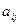
| … | 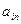
| 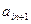
| |||
| … | … | … | … | … | … | … | … | … | … | … | … |
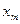
| … | … | 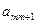
| … | 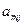
| … | 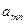
| 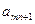
| |||
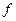
| … | … | 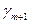
| … | 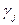
| … | 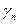
| 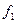
|
Числа 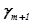 ,
,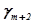 ,...,
,...,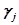 ,...,
,...,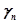 называются индексами; последняя строка таблицы называется индексной.
называются индексами; последняя строка таблицы называется индексной.
Полагая переменные (свободные) 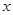
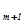 ,
, 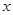
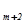 ...,xn равными нулю, получим первое базисное решение (a
...,xn равными нулю, получим первое базисное решение (a 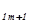 , a
, a 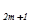 ,…, a
,…, a 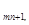 0...,0) и первое значение f
0...,0) и первое значение f  целевой функции, соответствующее этому решению. Первый базисный план и первое значение целевой функции образуют последний правый столбец таблицы 2.2. В верхней нулевой строке таблицы 2.2 записаны все переменные задачи ЛП, в левом нулевом столбце записаны базисные переменные. Будем рассматривать задачу на максимум функции f.
целевой функции, соответствующее этому решению. Первый базисный план и первое значение целевой функции образуют последний правый столбец таблицы 2.2. В верхней нулевой строке таблицы 2.2 записаны все переменные задачи ЛП, в левом нулевом столбце записаны базисные переменные. Будем рассматривать задачу на максимум функции f.
Переход ко второй симплекс-таблице осуществляется следующим образом: выбираем j -й столбец (разрешающий) таблицы 2.2 из условия, что 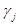 является наибольшим по модулю отрицательным индексом и хотя бы один из элементов a
является наибольшим по модулю отрицательным индексом и хотя бы один из элементов a 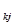 >0;
>0;
выбираем i -ю строку (разрешающую) из условия, что:
a 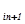 / a
/ a 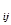 =
=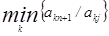 для a
для a 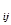 >0,
>0,
принимая a 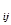 в качестве разрешающего элемента, производим преобразование коэффициентов таблицы
в качестве разрешающего элемента, производим преобразование коэффициентов таблицы
(в том числе элементов индексной строки) так, как это делается при решении системы уравнений методом Жордана-Гаусса:
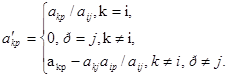
Таким образом, осуществляется переход от одного базисного решения системы ограничений к другому, от одной системы уравнений к другой, ей эквивалентной. При этом после преобразования в индексной строке получаются индексы, соответствующие новым свободным переменным. Переход к следующей таблице (если это необходимо) осуществляется аналогичным образом.
Сформулируем критерий оптимальности решения задачи ЛП с использованием симплекс-таблиц.
Если в очередной симплекс-таблице:
1) найдется хотя бы один отрицательный индекс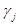 и в каждом столбце с отрицательным индексом окажется хотя бы один положительный элемент, то план можно улучшить, перейдя к следующей симплекс-таблице;
и в каждом столбце с отрицательным индексом окажется хотя бы один положительный элемент, то план можно улучшить, перейдя к следующей симплекс-таблице;
2) найдется хотя бы один отрицательный индекс 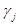 и все элементы в столбце, содержащем этот индекс отрицательные, то
и все элементы в столбце, содержащем этот индекс отрицательные, то
fmax =+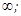
3) нет ни одного отрицательного индекса, то достигнут оптимальный план.
Пример. Найти наибольшее значение функции
f = 5 x  + 2 x
+ 2 x 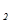 , если x
, если x  , x
, x 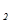 неотрицательные и удовлетворяют системе неравенств:
неотрицательные и удовлетворяют системе неравенств:
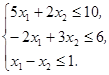
Решение. Вводим балансовые переменные х3, x 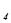 , x
, x 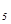 и получаем систему уравнений:
и получаем систему уравнений:
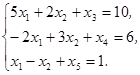
Целевую функцию представим в форме:
f = 0 - (-5x  - 2х
- 2х 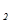 ). Составляем первую симплекс-таблицу 2.3:
). Составляем первую симплекс-таблицу 2.3:
Таблица 2.3
| Б.п. | 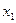
| 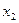
| 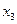
| 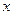 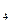
| 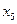
| с.к. |
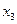
| ||||||
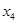
| -2 | |||||
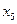
| 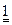
| -1 | ||||
| f | -5 | -2 |
В качестве разрешающего столбца выбираем первый столбец, ибо 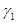 = -5-наибольший по модулю отрицательный индекс. В качестве разрешающей выбираем третью строку, так как min
= -5-наибольший по модулю отрицательный индекс. В качестве разрешающей выбираем третью строку, так как min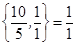 .
.
Значит, разрешающим элементом является элемент а 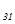 = 1. Переменная х
= 1. Переменная х  переводится в состав базисных вместо х
переводится в состав базисных вместо х 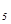 .Элементы разрешающей строки делим на 1(они не изменятся), элементы разрешающего столбца, кроме а
.Элементы разрешающей строки делим на 1(они не изменятся), элементы разрешающего столбца, кроме а  , заменяем нулями. Все другие элементы преобразуем по формуле:
, заменяем нулями. Все другие элементы преобразуем по формуле:
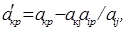
где
i = 3, j =1, k 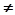 3, p
3, p 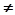 1.
1.
Формулу эту называют «правилом прямоугольника», ибо ее легко запомнить, пользуясь прямоугольником:
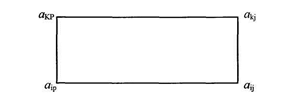
Правило для запоминания формулы: для получения новой вершины а '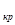 прямоугольника надо из старой вершины а
прямоугольника надо из старой вершины а 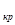 вычесть произведение a
вычесть произведение a 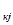 а
а 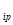 двух взаимно противоположных других вершин прямоугольника, деленное на вершину a
двух взаимно противоположных других вершин прямоугольника, деленное на вершину a 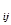 , противоположную старой вершине а
, противоположную старой вершине а 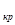 .
.
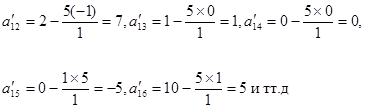
В результате получаем следующую таблицу 2.4:
Таблица 2.4
| Б.п | х1 | х2 | х3 | х4 | х5 | С.к |
| х3 | –5 | |||||
| х4 | ||||||
| х1 | –1 | |||||
| f | –7 |
Снова выбираем разрешающий столбец по максимуму модуля отрицательного индекса, им будет второй столбец.
Так как min 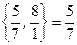 , то первая строка будет разрешающей.
, то первая строка будет разрешающей.
Переменную х 2 вводим в состав базисных вместо х3. Элементы первой строки делим на разрешающий элемент а12 = 7. Элементы второго столбца, кроме а12, заменяем нулями. Все остальные элементы таблицы 3 преобразуем по «правилу прямоугольника». Получим в результате таблицу 2.5.
Таблица 2.5
| Б.п. | х1 | х2 | х3 | х4 | х5 | С.к. |
| х 2 | 1/7 | -5/7 | 5/7 | |||
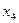
| -1/7 | 19/7 | 51/7 | |||
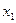
| 1/7 | 2/7 | 12/7 | |||
| f |
Так как в последней строке таблицы 5 нет отрицательных индексов, то f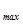 = 10 и (12/7; 5/7) – оптимальный план.
= 10 и (12/7; 5/7) – оптимальный план.
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 296; Нарушение авторских прав?; Мы поможем в написании вашей работы!