
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. Вводим балансовые переменные х3, х4 и получаем систему:
|
|
|
|
Вводим балансовые переменные х 3, х 4 и получаем систему:

Далее процесс решения мы представляем в виде симплексных таблиц, опуская подробные вычисления.
Таблица 2.20
| х 1 | х 2 | х 3 | х 4 | ||
| х 3 | -1 | ||||
| х 4 | -1 | ||||
| f | -16 |
Таблица 2.21
| х 1 | х 2 | х 3 | х 4 | ||
| х 2 | 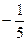
| 
| |||
| х 4 | 
| 
| |||
| f | 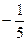
| 
| 
|
Таблица 2.22
| х 1 | х 2 | х 3 | х 4 | ||
| х 2 | 
| 
| 
| ||
| х 1 | 
| 
| 
| ||
| f | 
| 
| 
|
Без учета целочисленности . Так как дробная часть числа
. Так как дробная часть числа  больше дробной части числа
больше дробной части числа , то неравенство Гомори составляем исходя из уравнения
, то неравенство Гомори составляем исходя из уравнения  и записываем новую задачу.
и записываем новую задачу.
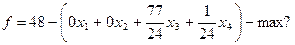

Введя балансовую переменную х 5 в неравенство последней системы, решаем эту задачу с помощью симплексных таблиц. При этом третье уравнение системы записываем так:  .
.
Таблица 2.23
| х 1 | х 2 | х 3 | х 4 | х 5 | ||
| х2 | 
| 
| 
| |||
| х 1 | 
| 
| 
| |||
| х 5 | 
| 
| 
| |||
| f | 
| 
| 
|
Разрешающий элемент таблицы 23 находим по максимуму модуля отрицательного коэффициента при аргументах в добавленном уравнении.
В силу этого фиктивная переменная х 5 сразу же выводится из состава базисных переменных и мы переходим к очередным симплексным таблицам.
Таблица 2.24
| х 1 | х 2 | х 3 | х 4 | х 5 | ||
| х 2 | ||||||
| х 1 | 1/5 | 1/5 | ||||
| х 3 | 1/5 | -24/5 | ||||
| f | -3/5 | 77/5 |
Таблица 2.25
| х 1 | х 2 | х 3 | х 4 | х 5 | ||
| х 2 | ||||||
| х 4 | ||||||
| х 3 | -1 | -5 | ||||
| f |
Так как среди индексов в последней таблице нет отрицательных элементов, то план (0;3; 0; 15; 0) является оптимальным. Таким образом f max = f (0; 3) = 48, при этом (0; 3) – целочисленное решение.
Пример. f =3 x 1 + x 2®max?
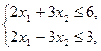
x 1, х 2 – целые неотрицательные.
Решение. Вводим балансовые переменные х 3, х 4, получаем систему:

Решаем задачу симплексным методом с помощью таблиц.
Таблица 2.26
| х 1 | х 2 | х 3 | х 4 | ||
| х 3 | |||||
| х 4 | -3 | ||||
| f | -3 | -1 |
Таблица 2.27
| х 1 | х 2 | х 3 | х 4 | ||
| х 3 | -1 | ||||
| х 1 | 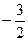
| 
| 
| ||
| f | 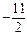
| 
| 
|
Таблица 2.28
| х 1 | х 2 | х 3 | х 4 | ||
| х 2 | 
| 
| 
| ||
| х 1 | 
| 
| 
| ||
| f | 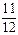
| 
| 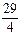
|
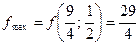 (без учета целочисленности аргументов).
(без учета целочисленности аргументов).
Так как 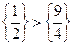 , то составляем неравенство Гомори для уравнения
, то составляем неравенство Гомори для уравнения 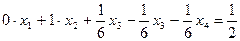 . Оно имеет вид:
. Оно имеет вид:  , или
, или 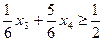 . Вводим фиктивную переменную х 5 такую, чтобы
. Вводим фиктивную переменную х 5 такую, чтобы  , или
, или  . Последнее уравнение включаем в систему ограничений и переходим к следующей симплексной таблице.
. Последнее уравнение включаем в систему ограничений и переходим к следующей симплексной таблице.
Таблиц 2.29
| х 1 | х 2 | х 3 | х 4 | х 5 | ||
| х 2 | 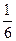
| 
| 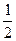
| |||
| х 1 | 
| 
| 
| |||
| х 5 | 
| 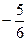
| 
| |||
| f | 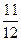
| 
| 
|
В таблице 29 разрешающий элемент находим по максимуму модуля отрицательного коэффициента при неизвестных добавленного уравнения, в рассматриваемом случае он равен ( ). Переходим к очередной таблице.
). Переходим к очередной таблице.
Таблица 2.30
| х 1 | х 2 | х 3 | х 4 | х 5 | ||
| х 2 | 
| 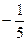
| 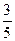
| |||
| х 1 | 
| 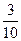
| 
| |||
| х 4 | 
| 
| 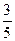
| |||
| f | 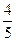
| 
| 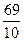
|
Так как  , то неравенство Гомори имеет вид:
, то неравенство Гомори имеет вид:  , т.е.
, т.е.  . Добавляем фиктивную переменную х 6 такую, чтобы
. Добавляем фиктивную переменную х 6 такую, чтобы 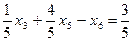 или
или  и переходим к следующей симплексной таблице.
и переходим к следующей симплексной таблице.
Таблица 2.31
| х 1 | х 2 | х 3 | х 4 | х 5 | х 6 | ||
| х 2 | 
| 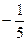
| 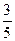
| ||||
| х 1 | 
| 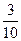
| 
| ||||
| х 4 | 
| 
| 
| ||||
| х 6 | 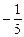
| 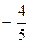
| 
| ||||
| f | 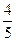
| 
| 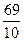
|
Теперь к последующим таблицам переходим без подробных объяснений.
Таблица 2.32
| х 1 | х 2 | х 3 | х 4 | х 5 | х 6 | ||
| х 2 | 
| 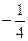
| 
| ||||
| х 1 | 
| 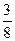
| 
| ||||
| х 4 | 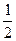
| 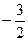
| 
| ||||
| х 5 | 1/4 | -5/4 | 3/4 | ||||
| f | 5/8 | 7/8 | 51/8 |
Таблица 2.33
| х 1 | х 2 | х 3 | х 4 | х 5 | х 6 | х 7 | ||
| х 2 | 
| 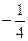
| 
| |||||
| х 1 | 
| 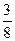
| 
| |||||
| х 4 | 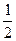
| 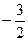
| 
| |||||
| х 5 | 
| 
| 
| |||||
| х 7 | 
| 
| 
| |||||
| f | 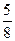
| 
| 
|
Таблица 2.34
| х 1 | х 2 | х 3 | х 4 | х 5 | х 6 | х 7 | ||
| х 2 | 
| 
| 
| |||||
| х 1 | ||||||||
| х 4 | -4 | |||||||
| х 5 | 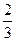
| 
| 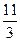
| |||||
| х 6 | 
| 
| 
| |||||
| f | 
| 
| 
|
Таблица 2.35
| х 1 | х 2 | х 3 | х 4 | х 5 | х 6 | х 7 | х 8 | ||
| х 2 | 
| 
| 
| ||||||
| х 1 | |||||||||
| х 4 | -4 | ||||||||
| х 5 | 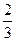
| 
| 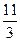
| ||||||
| х 6 | 
| 
| 
| ||||||
| х 8 | 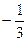
| 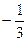
| 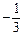
| ||||||
| f | 
| 
| 
|
Таблица 2.36
| х 1 | х 2 | х 3 | х 4 | х 5 | х 6 | х 7 | х 8 | ||
| х 2 | -1 | ||||||||
| х 1 | |||||||||
| х 4 | -5 | ||||||||
| х 5 | 
| ||||||||
| х 6 | -3 | ||||||||
| х 3 | -3 | ||||||||
| f |
Из последней таблицы видно, что f max= f (1, 1) = 4, где х 1=1, х 2 = 1 – целые числа.
РАЗДЕЛ 3. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Тема 3.1. Квадратичное программирование
Под задачей квадратичного программирования будем понимать задачу на отыскание оптимума целевой функции в следующих трех случаях:
1) целевая функция линейная, а ограничения на ее аргументы квадратичные;
2) целевая функция квадратичная, а ограничения на ее аргументы линейные;
3) целевая функция квадратичная и ограничения на ее аргументы квадратичные.
Рассмотрим несколько примеров решения таких задач в случае целевой функции двух аргументов.
Пример. F = 2 x 1 + 3 x 2®оптимум,

Решение. Находим и строим область ограничений.
Парабола  имеет вершину в точке V (2; 0) и ограничивает область решения системы неравенств сверху. Слева и снизу область ограничена осями координат.
имеет вершину в точке V (2; 0) и ограничивает область решения системы неравенств сверху. Слева и снизу область ограничена осями координат.
Задаем значения целевой функции. Пусть f = 0. Строим опорную прямую (линию одного уровня) 2 х 1 + 3 х 2 = 0. Она проходит через точки (0; 0) и (-3; 2). Двигая опорную прямую параллельно самой себе, находим точки входа и выхода О, А.
 Рис 3.1. Графический метод.
Рис 3.1. Графический метод.
При этом f (0; 0) = 2×0 + 3×0 = 0 – наименьшее значение целевой функции, а f (А) – ее наибольшее значение. Теперь находим координаты точки А. Угловой коэффициент касательной к параболе в точке А равен  , он же равен значению производной квадратичной функции
, он же равен значению производной квадратичной функции  в точке А. Таким образом
в точке А. Таким образом  . Следовательно,
. Следовательно,  и
и 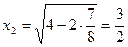 и значит,
и значит, 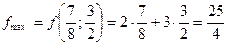 .
.
Пример. 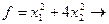 оптимум?
оптимум?
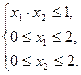
Решение. Находим и строим область решения системы неравенств. Так как уравнения х 1× х 2 = 1; х 1 = 0; х 1 = 2; х 2 = 0; х 2 = 2 задают на плоскости координат гиперболу и прямые, то криволинейный четырехугольник ОАВСD является областью решения системы неравенств.

Рис 3.2. Графический метод
Если f = 0, то уравнение  определяет начало координат, если f >0, то оно определяет эллипс
определяет начало координат, если f >0, то оно определяет эллипс
 с полуосями
с полуосями 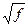 и
и 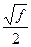 .
.
Таким образом линии одинакового уровня (одинакового значения целевой функции) представляют собой подобные эллипсы с центром подобия в начале координат. Чем крупнее эллипс, тем больше значение целевой функции. Получаем, что
fmin = f (O) = 0 и 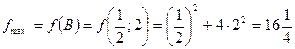 .
.
Пример.  оптимум?
оптимум?

Решение. Область решения системы неравенств является четырехугольник АВСD (рис. 3.3.).
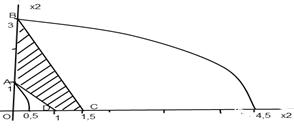
Рис. 3.3. Геометрический метод
Линией одинакового значения целевой функции является парабола  , с вершиной в точке
, с вершиной в точке  . При движении параболы в положительном направлении оси Ох
. При движении параболы в положительном направлении оси Ох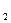 значение f будет увеличиваться. Исходя из этого имеем:
значение f будет увеличиваться. Исходя из этого имеем:
 f max = f (B) = f (0; 3) = 2×0 + 32 = 9.
f max = f (B) = f (0; 3) = 2×0 + 32 = 9.
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 717; Нарушение авторских прав?; Мы поможем в написании вашей работы!