
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 2.9. Метод потенциалов
|
|
|
|
Из математической формулировки транспортной задачи видно, что она является частным случаем задачи линейного программирования, и, следовательно, для ее решения можно применять, например, симплексный метод. Однако, в силу особенностей, транспортная задача допускает ряд более простых методов решения. К числу таких методов относится метод потенциалов, который был впервые сформулирован
Л.В. Канторовичем. Рассмотрим применение этого метода при следующих данных:
а 1=250, а 2 = 200, а 3 = 50, b 1 = 50, b 2 = 100, b 3 = 150, b 4=120, b 5 = 80,
С = 
где С – матрица тарифов.
Данные задачи группируем в таблицу 2.6:
Таблица 2.6
 b j
ai b j
ai
| |||||
Находим первое базисное решение (первый план перевозок) методом северо-западного угла. Для этого максимально «загружаем» клетку (1,1), помещая туда 50 т. При этом спрос первого потребителя полностью удовлетворяется, первый столбец «закрываем». Заметим, что если бы на первом складе было бы меньше груза, чем требуется первому потребителю, то освободился бы полностью первый склад и мы бы «закрыли» первую строку, а недостающий груз первому потребителю был бы поставлен со второго склада, а при необходимости последовательно еще и с других складов. Теперь максимально «загружаем» клетку (1,2), помещая туда 100 т. Так как при этом спрос второго потребителя удовлетворяется полностью, то второй столбец «закрываем». Максимально загружаем клетку (1,3), помещая туда оставшиеся на первом складе 100 т. После этого первая строка «закрыта». Теперь распределяем груз из второго склада. Максимально загружаем клетку (2,3), помещая туда 50 тонн. Так как после этого спрос третьего потребителя полностью удовлетворяется, то «закрываем» третий столбец.
Максимально загружаем клетку (2, 4), помещая туда 120 тонн. Тогда четвертый столбец будет «закрыт». Максимально загружаем клетку (2, 5), помещая туда оставшиеся на втором складе 30 тонн. Теперь остается весь груз из третьего склада отдать пятому потребителю и его спрос будет удовлетворен, т.е. в клетку (3,5) помещаем 50 тонн. В результате получаем первый план перевозок, содержащийся в таблице 2.7.
Таблица 2.7
 bi
ai bi
ai
| |||||
| 100-l | l | ||||
| 50+l | 30 -l | ||||
Количество базисных переменных равно: m + n -1=3+5-1=7.
В данном случае базисными переменными являются величины х 11, х 12, х 13, х 23, х 24,, х 25, х 35, соответствующие «загруженным» клеткам.
Транспортные расходы выражаются формулой:
f = 
Вопрос о том, можно ли улучшить план перевозок путем перехода к новому базисному решению системы ограничений транспортной задачи зависит от знаков коэффициентов gpq в выражении
f = f 0 +  ,
,
где хpq – свободные переменные, f 0 – транспортные расходы по начальному плану перевозок.
Если хотя бы один из коэффициентов gpq <0, то транспортные расходы можно уменьшить, в противном случае - план перевозок будет оптимальным.
Каждой загруженной клетке(i, j) поставим в соответствие величины Ui, Vj, которые вычисляются из уравнений:
Ui + Vj = сij.
В рассматриваемом случае число уравнений равно
m + n–1= 7, а число неизвестных Ui, Vj равно m + n = 8. Так как число неизвестных больше числа уравнений на единицу, то одной из неизвестных можно дать произвольное значение, например, 0.
Обозначим через с¢pq (косвенный тариф) сумму UP+ V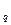 где (p, q) – пустая клетка. Можно доказать, что знак gpq = сpq – с¢pq.
где (p, q) – пустая клетка. Можно доказать, что знак gpq = сpq – с¢pq.
Величины Ui, Vj называют потенциалами и в силу этого метод решения транспортной задачи носит название метода потенциалов.
Составляем систему уравнений и находим потенциалы.
U 1 + V 1 = 10, U 1 = 0, V 1=10,
U 1 + V 2 = 12, U 2 = -11, V 2 = 12,
U 1 + V 3 = 15, U 3 = -17. V 3 = 15,
U 2 + V 3 = 4, V 4 = 25,
U 2 + V 4 = 14, V 5 = 41.
U 2 + V 5 = 30,
U 3 + V 5 =24.
Находим величины с¢pq, 




Так как некоторые из величин gpq отрицательные, то план можно улучшить. «Загружаем» клетку (1;5), ибо g 15 – наибольший по модулю отрицательный коэффициент, помещая туда l тонн, и перераспределяем поставки груза. Перераспределение груза осуществляется по выбранному контуру с таким расчетом, чтобы транспортные затраты уменьшились.
Так как поставки груза не могут быть отрицательными, то самое большое значение для l равно 30. Вычислим насколько уменьшаются транспортные затраты.
5 l - 15 l +4 l- 30 l /= /-36l/ =36l =36× 30 =1080.
Таким образом, такое перераспределение поставок груза целесообразно и мы получаем второй, более лучший план поставок (таблица 2.8).
Таблица 2.8
 bi
ai bi
ai
| |||||
Снова проверяем, можно ли улучшить план поставок груза. Для этого составляем систему уравнений и находим потенциалы по загруженным клеткам.
Теперь мы не будем так подробно составлять и решать очередную систему уравнений. Для этого добавим к предыдущей таблице стоку и столбец потенциалов. Получим таблицу 2.9.
Таблица 2.9
| bi ai | 
| |||||
70 - 
| 5 30+
|  = 0 = 0
| ||||
| -1 |
80 +
|
120-
| -6 | 
| ||

| 24 50-
|  = 19 = 19
| ||||

| 
| 
| 
| 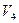 = 25 = 25
| 
|
Так как в первой строке наибольшее количество «загруженных» клеток, то положим  = 0. Тогда из равенства
= 0. Тогда из равенства  , пользуясь соответствующими «г-образными дорожками» последовательно находим, что
, пользуясь соответствующими «г-образными дорожками» последовательно находим, что
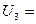 24 - 5 = 19,
24 - 5 = 19,  = 4 - 15 = - 11,
= 4 - 15 = - 11, 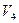 =14 – (-11) = 25.
=14 – (-11) = 25.
Находим косвенные тарифы с¢pq.

Найденные косвенные тарифы размещаем в не загруженных клетках соответствующей таблицы напротив фактических тарифов.
Находим величины gpq.

Так как g34 – наибольший по модулю отрицательный коэффициент, то «загружаем» клетку (3;4), помещая туда l тонн, и перераспределяем поставки груза. Выбираем контур, соединяющий клетки (3;4), (3;5),(1;5), (1;3), (2;3),(2;4) в таблице 9.
Перераспределение поставок по этому контуру дает уменьшение транспортных расходов на 26 l, где l = 50. В результате получаем третий план перевозок (таблица 2.10).
Таблица 2.10
| bj ai | 
| |||||
| 20- l | l | |||||
| -1 | -1 | 130 + l | 70 - l | -6× | -11 | |
| -2 | -7 | |||||

|
Проверяем, можно ли улучшить третий план перевозок. Для этого находим потенциалы и косвенные тарифы (таблица 2.10).
Загружаем клетку (1;4) так как только g 14< 0.
Выбираем контур и осуществляем перераспределение поставок груза (таблица 2.10). Транспортные расходы при этом уменьшаются на величину 5 l, где l = 20. Получаем четвертый план перевозок груза.
Таблица 2.11
bj
 ai
ai
|  
| |||||
| -1 | --6 | |||||
| --2 | ||||||

|
Проверяем, можно ли улучшить четвертый план перевозок. Для этого находим потенциалы и косвенные тарифы (таблица 2.11).
Так как gpq > 0, т.е. косвенные тарифы для каждой пустой клетки не превышают соответствующих фактических тарифов, то четвертый план является оптимальным. Наименьшие транспортные расходы составляют:
50×10 + 100×12 + 20×20 + 80×5 + 150×4 + 50×14 + 50×18 = 4700.
Часто оптимальный план достигается быстрее, если первоначальный план перевозок находят не методом северо-западного угла, а методом наименьшего расстояния (методом наименьшего тарифа). Суть его состоит в том, что максимально «загружают» клетку, соответствующую наименьшему расстоянию, в результате «закрывается» либо строка, либо столбец, на пересечении которых она находится. Из оставшихся клеток заполняют ту, которая соответствует наименьшему расстоянию и т.д. Для подтверждения сказанного решим рассмотренную нами задачу снова.
Составляем первый план перевозок по методу наименьшего тарифа. Первой «загружается» клетка (2;3) и третий столбец закрывается. Затем «загружается» клетка (1;5)) и пятый столбец закрывается. Далее «загружается» клетка (2;1) и закрывается первый столбец и вторая строка. Потом «загружается» клетка (1;2) и закрывается второй столбец. Затем «загружаются» клетки (3;4) и (1;4). В результате получаем первый план перевозок груза, которому соответствуют транспортные расходы 4800.
Таблица 2.12
 bj
ai bj
ai
|

| |||||
| l | 70- l | |||||
| 50- l | l | |||||
| -2 | ||||||

|
Находим потенциалы Ui, Vj и косвенные тарифы.
«Загружаем» клетку (2;4), ибо g 24 – наибольший по модулю отрицательный коэффициент.
Выбираем контур перераспределения груза и при l = 50 приходим к полученному нами ранее оптимальному плану перевозок
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 350; Нарушение авторских прав?; Мы поможем в написании вашей работы!